��Ŀ����
����Ŀ����ͼ![]() ���߶�
���߶�![]() ��
��![]() �ཻ��
�ཻ��![]() ������
������![]() ��
��![]() �����ǰ�����ͼ
�����ǰ�����ͼ![]() ��ͼ�γ�֮Ϊ��
��ͼ�γ�֮Ϊ��![]() �����Σ���ͼ
�����Σ���ͼ![]() ����ͼ
����ͼ![]() �������£�
�������£�![]() ��
��![]() ��ƽ����
��ƽ����![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��������
��������![]() ��
��![]() �ֱ��ཻ��
�ֱ��ཻ��![]() ��
��![]() ���Խ���������⣺
���Խ���������⣺
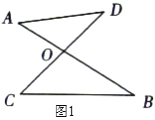
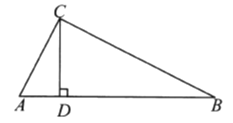
(1)��ͼ![]() �У���ֱ��д��
�У���ֱ��д��![]() ��
��![]() ��
��![]() ��
��![]() ֮���������ϵ��__________
֮���������ϵ��__________
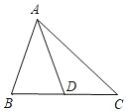
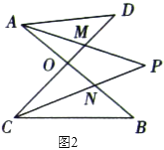
(2)��ϸ�۲죬��ͼ![]() ����
����![]() �����εĸ�����______����
�����εĸ�����______����
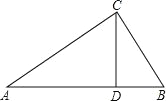
(3)ͼ![]() �У���
�У���![]() �ȣ�
�ȣ�![]() ��ʱ����
��ʱ����![]() �Ķ���.
�Ķ���.
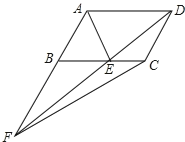
(4)ͼ![]() ��
��![]() ��
��![]() Ϊ�����ʱ�������������䣬����
Ϊ�����ʱ�������������䣬����![]() ��
��![]() ��
��![]() ֮�������������������ϵ��(ֱ��д�����������֤��)
֮�������������������ϵ��(ֱ��д�����������֤��)
���𰸡�(1)![]() ��(2)6��(3)
��(2)6��(3)![]() ��(4)
��(4)![]() .
.
��������
(1)���������ε��ڽǺͶ����Լ��Զ��������ʽ�������ɵý⣻
(2)���ݶ����ҳ���8���Ρ��ĸ������ɣ�
(3)���ݽ�ƽ���ߵĶ���ɵá�1=��2����3=��4��������![]() ���������ʿɵã�
���������ʿɵã�![]() ����
����![]() �����̶��ɵ�
�����̶��ɵ�![]() ������������ݼ�����ô𰸣�
������������ݼ�����ô𰸣�
(4)����(3)���Ƶ�����������ý���.
(1)���������ε��ڽǺͶ�������AOD+��A+��D=180�㣬��BOC+��B+��C=180�㣬
�ߡ�AOD=��BOC(�Զ������)��
��![]() ��
��
�ʴ�Ϊ����A+��D=��B+��C��
(2) �Ե�OΪ�������8�������С�AOD�͡�BOC����AOM�͡�CON����AOD�͡�CON����AOM�͡�BOC��
�Ե�MΪ�������8�������С�ADM�͡�CMP��
�Ե�NΪ�������8�������С�ANP�͡�BCN��
����6����
�ʴ�Ϊ��6��
(3)��ͼ2��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��
����1=��2����3=��4��
������![]() ���������ʿɵã�
���������ʿɵã�
![]() ����
����
![]() ����
����
����![]() ���ã�
���ã�
![]() ��
��
![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
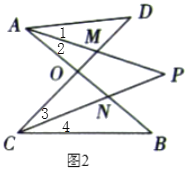
(4)![]() ���������£�
���������£�
��ͼ2��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��
���1=��2����3=��4��
������![]() ���������ʿɵã�
���������ʿɵã�
![]() ����
����
![]() ����
����
����![]() ���ã�
���ã�
![]() ��
��
��![]() .
.

����Ŀ��ij��ѧ��������У��,��Ǩ����У��ǰ��У300��ѧ����ε�У���������һ�ε���,���õ���������:
���� | 65�� |
�����г� | 100�� |
���������� | 125�� |
���� | 10�� |
����
����������ݷֱ��Ƴ�����ͳ��ͼ������ͳ��ͼ.