题目内容
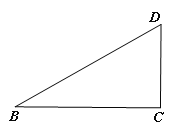
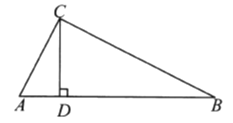
【题目】如图,在![]() 中,
中, ![]() ,CD是斜边AB上的高.
,CD是斜边AB上的高.
(1)证明: ![]() ∽
∽![]()
(2)写出除(1)外的另两对相似三角形.
(3)AC是哪两条线段的比例中项?请简要证明(说明).
【答案】(1)证明见解析;(2)△ABC ∽ △CBD,△ACD ∽ △CBD;(3)AC是AD和AB的等比中项,证明见解析.
【解析】试题分析:(1)求出∠CDA=∠ACB=90°,根据有两个角对应相等的两三角形相似得出△ACD∽△ABC.
(2)根据相似三角形的判定可得出△ABC ∽ △CBD,△ACD ∽ △CBD;
(3)根据三角形相似得到比例式,由比例式化成等积式即可.
试题解析:(1)证明:∵∠ACB=90°,CD⊥AB,
∴∠CDA=∠ACB=90°,
∵∠A=∠A,
∴△ACD∽△ABC,
(2) △ABC ∽ △CBD,△ACD ∽ △CBD
(3) AC是AD和AB的等比中项,
证明: ∵△ABC∽△ACD,
∴![]() ,
,
∴AC2=ABAD,
∴AC是AB,AD的比例中项,

练习册系列答案
相关题目