题目内容
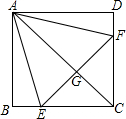 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,△CEF与△ABE的面积比为( )
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,△CEF与△ABE的面积比为( )| A、3:2 | B、2:1 |
| C、5:3 | D、无法确定 |
考点:正方形的性质,全等三角形的判定与性质,等边三角形的性质,勾股定理
专题:计算题
分析:易证Rt△ABE≌Rt△ADF,从而得到BE=DF,进而得到CE=CF.设BE=x,CE=y,在Rt△ABE中,运用勾股定理就可得到2x2+2xy=y2.从而可以求出△CEF与△ABE的面积比.
解答:解:∵四边形ABCD是正方形,△AEF是等边三角形,
∴∠B=∠BCD=∠D=90°,AB=BC=DC=AD,AE=AF=EF.
在Rt△ABE和Rt△ADF中,
.
∴Rt△ABE≌Rt△ADF(HL).
∴BE=DF.
∴CE=CF.
设BE=x,CE=y,
则CF=CE=y,AB=BC=x+y,AE=EF=
y.
在Rt△ABE中,
∵∠B=90°,AB=x+y,BE=x,AE=
y,
∴(x+y)2+x2=(
y)2.
整理得:2x2+2xy=y2.
∴S△CEF:S△ABE
=(
CE•CF):(
AB•BE)
=(CE•CF):(AB•BE)
=y2:[(x+y)x]
=(2x2+2xy):(x2+xy)
=2:1.
故选:B.
∴∠B=∠BCD=∠D=90°,AB=BC=DC=AD,AE=AF=EF.
在Rt△ABE和Rt△ADF中,
|
∴Rt△ABE≌Rt△ADF(HL).
∴BE=DF.

∴CE=CF.
设BE=x,CE=y,
则CF=CE=y,AB=BC=x+y,AE=EF=
| 2 |
在Rt△ABE中,
∵∠B=90°,AB=x+y,BE=x,AE=
| 2 |
∴(x+y)2+x2=(
| 2 |
整理得:2x2+2xy=y2.
∴S△CEF:S△ABE
=(
| 1 |
| 2 |
| 1 |
| 2 |
=(CE•CF):(AB•BE)
=y2:[(x+y)x]
=(2x2+2xy):(x2+xy)
=2:1.
故选:B.
点评:本题考查了正方形的性质、等边三角形的性质、全等三角形的判定与性质、勾股定理等知识,而采用整体思想(把x2+xy看成一个整体)是解决本题的关键.

练习册系列答案
相关题目
若x2-mxy+9y2是一个完全平方式,则m的值是( )
| A、8 | B、6 | C、±8 | D、±6 |
下列调查中,适宜采用全面调查(普查)方式的是( )
| A、调查中国好声音的收视率 |
| B、调查我国各级党委落实中央“八项规定”的情况 |
| C、调查全国人民对“神十”发射的关注程度 |
| D、调查本校各办公室保险盒的老化情况 |
( )
| A、30°角 | B、60°角 |
| C、90°角 | D、150°角 |
下列调查中,适合采用全面调查方式的是( )
| A、对宜春秀江水质情况的调查 |
| B、对某班50名同学体重情况的调查 |
| C、对端午节期间市场上粽子质量情况的调查 |
| D、对万载县某类烟花爆竹燃放安全情况的调查 |
 如图,在平行四边形ABCD中,AC交BD于点O,点E、点F分别是OA、OC的中点,
如图,在平行四边形ABCD中,AC交BD于点O,点E、点F分别是OA、OC的中点,