题目内容
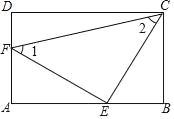
【题目】如图:在矩形ABCD中,E、F分别是AB、AD边上的点,且BE=AF,∠1=∠2.
(1)Rt△AEF与Rt△BCE全等吗?说明理由;
(2)△CEF是不是直角三角形?说明理由.
【答案】(1)结论:Rt△AEF与Rt△BCE全等(2)结论:△CEF是直角三角形.
【解析】试题分析:(1)根据HL,由BE=AF、EC=EF,即可证明;
(2)只要证明∠4+∠5=90°,即可解决问题;
试题解析:
(1)结论:Rt△AEF与Rt△BCE全等.
理由:在矩形ABCD中,∠A=∠B=90°
∵BE=AF,
∵∠1=∠2,
∴CE=EF
∴Rt△AEF≌Rt△BCE.
(2)结论:△CEF是直角三角形.
理由:∵Rt△AEF≌Rt△BCE.
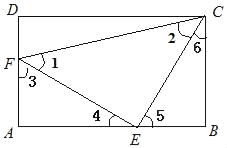
∴∠3=∠5,
∵∠3+∠4=90°,∠5+∠4=90°,
∴∠CEF=180°﹣(∠4+∠5)=180°﹣90°=90°,
所以△CEF是直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目