题目内容
 如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.下列结论错误的是
如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.下列结论错误的是
- A.∠ECD=∠EDC
- B.OC=OD
- C.△OCD是等边三角形
- D.OE是线段CD垂直平分线
C
分析:根据角平分线的性质利用排除法对四个选项进行逐一分析即可.
解答: 解:∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D,
解:∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D,
∴DE=CE,∠EOD=∠EOC,
在Rt△ODE与Rt△OCE中,
∵DE=CE,OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,故B选项正确;
在△ODF与△OCF中,
∵OD=OC,∠EOD=∠EOC,OF=OF,
∴△ODF≌△OCF,
∴∠ODC=∠OCD,
∵∠ODE=∠OCE,
∴∠ECD=∠EDC,故A选项正确;
∵△ODF≌△OCF,
∴DF=CF,
∴OE是线段CD的垂直平分线,故D选项正确.
故选C.
点评:本题考查的是角平分线的性质及全等三角形的判定与性质,熟知角的平分线上的点到角的两边的距离相等的知识是解答此题的关键.
分析:根据角平分线的性质利用排除法对四个选项进行逐一分析即可.
解答:
 解:∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D,
解:∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D,∴DE=CE,∠EOD=∠EOC,
在Rt△ODE与Rt△OCE中,
∵DE=CE,OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,故B选项正确;
在△ODF与△OCF中,
∵OD=OC,∠EOD=∠EOC,OF=OF,
∴△ODF≌△OCF,
∴∠ODC=∠OCD,
∵∠ODE=∠OCE,
∴∠ECD=∠EDC,故A选项正确;
∵△ODF≌△OCF,
∴DF=CF,
∴OE是线段CD的垂直平分线,故D选项正确.
故选C.
点评:本题考查的是角平分线的性质及全等三角形的判定与性质,熟知角的平分线上的点到角的两边的距离相等的知识是解答此题的关键.

练习册系列答案
相关题目
 63、如图,点P是∠AOB的平分线上的一点,作PD⊥OA,垂足为D,PE⊥OB垂足为E,DE交OC于点F.则在图中:
63、如图,点P是∠AOB的平分线上的一点,作PD⊥OA,垂足为D,PE⊥OB垂足为E,DE交OC于点F.则在图中: 24、如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
24、如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
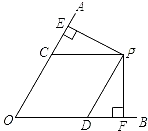 PF⊥OB,垂足分别为点E、F.
PF⊥OB,垂足分别为点E、F. 如图,点P是∠AOB内部一点,点P关于OA、OB的对称点是H、G,直线HG交OA、OB于点C、D,若HG=4cm,且∠AOB=30°,则△HOG的周长是
如图,点P是∠AOB内部一点,点P关于OA、OB的对称点是H、G,直线HG交OA、OB于点C、D,若HG=4cm,且∠AOB=30°,则△HOG的周长是