Question

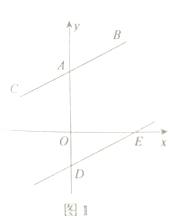
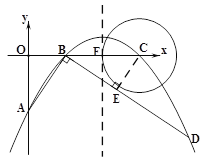
【题目】如图，在平面直角坐标系中，顶点为(4，1)的抛物线交y轴于点A，交x轴于B，C两点(点B在点C的左侧)，已知C点坐标为(6，0)．

(1)求此抛物线的解析式；

(2)连结AB，过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与抛物线的对称轴l相切，先补全图形，再判断直线BD与⊙C的位置关系并加以证明；

(3)已知点P是抛物线上的一个动点，且位于A，C两点之间．问：当点P运动到什么位置时，△PAC的面积最大？求出△PAC的最大面积．

Answer 1

【答案】(1)y＝－x2＋2x－3；(2) 直线BD与⊙C相离．证明见解析；(3) P点的位置是(3， )，△PAC的最大面积是.

【解析】

试题（1）根据顶点坐标列出顶点式，再将C点坐标代入即可；

（2）先求出圆的半径，再借助三角形相似，求出C到直线的距离，比较他们的大小即可；

（3）过点作平行于轴的直线交于点.设出点坐标，求出PQ的值，再表示出

的面积，借助函数关系式求出最值.

试题解析：（1）∵抛物线的顶点为（4,1）,

∴设抛物线解析式为.

∵抛物线经过点（6,0）,

∴.

∴.

∴.

所以抛物线的解析式为；

(2)补全图形、判断直线BD与⊙相离

令=0,则,.

∴点坐标（2,0）.

又∵抛物线交轴于点,

∴A点坐标为（0,-3）,

∴.

设⊙与对称轴l相切于点F,则⊙的半径CF=2,

作⊥BD于点E,则∠BEC=∠AOB=90°.

∵,

∴.

又∵,

∴.

∴∽,

∴.

∴,

∴.

∴直线BD与⊙相离；

(3)如图,过点作平行于轴的直线交于点.

∵A（0,-3）,（6,0）.

∴直线解析式为.

设点坐标为（,）,

则点的坐标为（,）.

∴PQ=-()=.

∵,

∴当时,的面积最大为

∵当时,=

∴点坐标为（3,）.

综上：点的位置是（3,）,的最大面积是.