题目内容
在梯形ABCD中,AB∥CD,E是BC的中点,连接DE、AE,试探索S△ADE和S梯形ABCD之间的数量关系,并证明.
考点:梯形
专题:
分析:延长DE至F点交AB延长线于F,根据ASA定理得出△DCE≌△FBE,根据全等三角形的性质得出S△DCE=S△FBE,故S梯形ABCD=S△DAF.由△ADE与△FAE的高相等即可得出结论.
解答: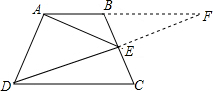 解:S△ADE=
解:S△ADE=
S梯形ABCD.
证明:延长DE至F点交AB延长线于F,
∵AB∥CD,
∴∠C=∠FBE.
∵E是BC的中点
∴BE=CE.
在△DCE与△FBE中,
,
∴△DCE≌△FBE(ASA),
∴S△DCE=S△FBE,
∴S梯形ABCD=S△DAF.
∵△DCE≌△FBE,
∴DE=EF.
∵△ADE与△FAE的高相等,
∴S△ADE=S△FAE=
S△DAF=
S梯形ABCD.
 解:S△ADE=
解:S△ADE=| 1 |
| 2 |
证明:延长DE至F点交AB延长线于F,
∵AB∥CD,
∴∠C=∠FBE.
∵E是BC的中点
∴BE=CE.
在△DCE与△FBE中,
|
∴△DCE≌△FBE(ASA),
∴S△DCE=S△FBE,
∴S梯形ABCD=S△DAF.
∵△DCE≌△FBE,
∴DE=EF.
∵△ADE与△FAE的高相等,
∴S△ADE=S△FAE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了梯形的性质,同时涉及全等三角形等知识,要正确作出辅助线才可解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
计算:
(1)7x+4(x2-2)-2(2x2-x+3);
(2)4ab-3b2-[(a2+b2)-(a2-b2)];
(3)(3mn-5m2)-(3m2-5mn);
(4)2a+2(a+1)-3(a-1).
(1)7x+4(x2-2)-2(2x2-x+3);
(2)4ab-3b2-[(a2+b2)-(a2-b2)];
(3)(3mn-5m2)-(3m2-5mn);
(4)2a+2(a+1)-3(a-1).
下列说法正确的是( )
| A、若a≠b,则a2≠b2 |
| B、零除以任何数都等于零 |
| C、任何负数都小于它的相反数 |
| D、两个负数比较大小,绝对值大的就大 |