题目内容
15.计算(1)$\sqrt{2}+\sqrt{3}(\sqrt{\frac{2}{3}}-\sqrt{3})$
(2)$\sqrt{12}+sin{45°}-cos{30°}-\sqrt{\frac{1}{2}}$.
分析 (1)先进行二次根式的乘法运算,然后合并即可;
(2)先把各二次根式化为最简二次根式和利用特殊角的三角函数值计算得到原式=2$\sqrt{3}$+$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{2}}{2}$,然后合并即可.
解答 解:(1)原式=$\sqrt{2}$+$\sqrt{3}$×$\frac{\sqrt{2}}{\sqrt{3}}$-$\sqrt{3}$×$\sqrt{3}$
=$\sqrt{2}$+$\sqrt{2}$-3
=2$\sqrt{2}$-3;
(2)原式=2$\sqrt{3}$+$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{2}}{2}$
=$\frac{3\sqrt{3}}{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知a=(-1)2016,b=-(-1.2),c=-32,则a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | b>a>c |
10.下表给出了二次函数y=-x2+bx+c中两个变量y与x的一些对应值:
(1)根据表格中的数据,确定b,c,n的值;
(2)直接写出抛物线y=-x2+bx+c的顶点坐标和对称轴;
(3)当y>0时,求自变量x的取值范围.
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 5 | n | c | 2 | -3 | -10 | … |
(2)直接写出抛物线y=-x2+bx+c的顶点坐标和对称轴;
(3)当y>0时,求自变量x的取值范围.
4.下列命题是真命题的是( )
| A. | 两个锐角之和一定是钝角 | B. | 如果x2>0,那么x>0 | ||
| C. | 两直线平行,同旁内角相等 | D. | 平行于同一条直线的两条直线平行 |
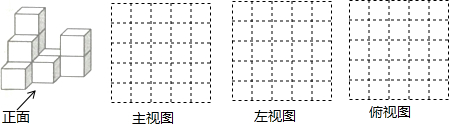
 如图,这是一个由5个正方体组成的立体图形,从上面看得到的平面图形是( )
如图,这是一个由5个正方体组成的立体图形,从上面看得到的平面图形是( )



