题目内容
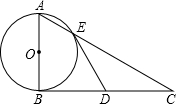
已知：如图，在△ABC中，AB=AC，点D是边BC的中点．以BD为直径作圆O，交边AB于点
P，连接PC，交AD于点E．
（1）求证：AD是圆O的切线；
（2）若PC是圆O的切线，BC=8，求DE的长．
P，连接PC，交AD于点E．（1）求证：AD是圆O的切线；
（2）若PC是圆O的切线，BC=8，求DE的长．
（1）证明：∵AB=AC，点D是边BC的中点，
∴AD⊥BD．
又∵BD是圆O直径，
∴AD是圆O的切线．
（2）连接OP，
由BC=8，得CD=4，OC=6，OP=2，
∵PC是圆O的切线，O为圆心，
∴∠OPC=90°．
由勾股定理，得PC=4
，
在△OPC中，tan∠OCP=
=
，
在△DEC中，tan∠DCE=
=
，DE=DC•
=
．
∴AD⊥BD．
又∵BD是圆O直径，
∴AD是圆O的切线．
（2）连接OP，
由BC=8，得CD=4，OC=6，OP=2，
∵PC是圆O的切线，O为圆心，
∴∠OPC=90°．
由勾股定理，得PC=4
| 2 |
在△OPC中，tan∠OCP=
| OP |
| CP |
| ||
| 4 |
在△DEC中，tan∠DCE=
| DE |
| DC |
| ||
| 4 |
| ||
| 4 |
| 2 |
练习册系列答案
名校课堂系列答案
相关题目
=4cm，AB=5cm，⊙O的半径R=4.5cm，此时P点到圆心O的距离是______cm．
