题目内容
我们规定:如果一条直线将一个平面图形分成面积相等的两部分,则这条直线被平面图形所截得的线段叫做该图形的直径.
(1)如图甲,已知PM=PN=13,MN=10,请求出△PMN的一条直径的长;
 (2)如图乙,已知DE是△ADC的直径,∠ADC=90°,∠BAC=∠ADE=60°,AC=2AB. 求证:△ABD≌△ECD.
(2)如图乙,已知DE是△ADC的直径,∠ADC=90°,∠BAC=∠ADE=60°,AC=2AB. 求证:△ABD≌△ECD.
解:(1)作CD⊥AB于点D.
∵AC=BC=13,∴CD 是AB的中线,
∴CD 是△ABC的一条直径,
又∵AB=10,∴AD=5,
∴直径CD=12;
(2)∵DE是△ADC的直径,∴AE=EC,
∵AC=2AB,∴AB =EC ,
∵∠ADC=90°∴AE=DE,
又∵∠BAC=∠ADE=60°
∴△ADE是等边三角形,
∴DA=DE,∠EAD=∠ADE=60°
∵∠BAD=∠BAC+∠DAC=120°, ∠CED=∠ADE+∠DAC=120°
∴∠BAD=∠DE C
C
∴△ABD≌△ECD(SAS)

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案以下是根据南京市国民经济和社会发展统计公报中的相关数据,绘制统计图的一部分.
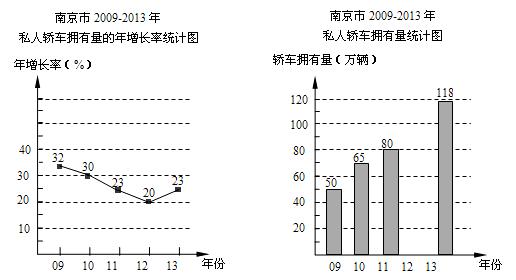
请根据以上信息解答下列问题:
(1)2012年南京市私人轿车拥有是多少万辆?
(2)补全条形统计图;
(3)经测定,汽车的碳排放量与汽车的排量大小有关.如驾驶排量1.6L的轿车,若一年行驶里程1万千米,则这一年,该轿车的碳排放量约为2.7吨.经调查,南京市某小区的300辆私人轿车,不同排量的数量统计如下表:
| 排量(L) | 小于1.6 | 1.6 | 1.8 | 大于1.8 |
| 数量(辆) | 30 | 150 | 62 | 58 |
请按照上述的统计数据,通过计算估计,2013年南京市仅排量为1.6L的私人轿车(假定每辆车平均一年行驶的路程都为1万千米)的碳排放总量约为多少万吨?
 如图,在等边
如图,在等边 中,
中, 为
为 边上一点,
边上一点, 为
为 边上
边上
 则
则

 ,
, 四个数中,是无理数的是…………………………【 】
四个数中,是无理数的是…………………………【 】 B.
B.  C.
C.  D.
D. 

 B.
B. C.
C. D.
D.
