题目内容
某学生每天早晨骑自行车上学,早晨7点准时出发,以某一速度匀速前进.一天早上,由于有事,停下耽误了几分钟为了按时到校,他加快了速度,仍匀速前进,结果准点到校.这位同学这天早上7点出发的路程S(千米)与时间t(小时)的函数图象如图所示,则这位同学准点到校的时间为( )
A.7点21分
B.7点18分
C.7点12分
D.7点30分
【答案】分析:求出OA的解析式,求出BC的解析式,两解析式的交点横坐标即为这位同学准点到校的时间.
解答: 解:设OA的解析式为y=kx,
解:设OA的解析式为y=kx,
将(0.1,1.5)代入解析式y=kx得
1.5=0.1k,
即k=15,
函数解析式为y=15x.
设函数BC解析式为y=mx+n,
将(0.2,1.5),(0.3,4)分别代入解析式y=mx+n得,
 ,
,
解得 ,
,
函数解析式为y=25x-3.5.
将为y=15x与y=25x-3.5组成方程组得
 ,
,
解得 .
.
故两函数交点坐标为(0.35,5.25).
则准点到校时间为7小时,0.35×60=21分.
故选A.
点评:本题考查了函数的图象,读懂函数图象的意义以及熟悉待定系数法求函数解析式是解题的关键.
解答:
 解:设OA的解析式为y=kx,
解:设OA的解析式为y=kx,将(0.1,1.5)代入解析式y=kx得
1.5=0.1k,
即k=15,
函数解析式为y=15x.
设函数BC解析式为y=mx+n,
将(0.2,1.5),(0.3,4)分别代入解析式y=mx+n得,
 ,
,解得
 ,
,函数解析式为y=25x-3.5.
将为y=15x与y=25x-3.5组成方程组得
 ,
,解得
 .
.故两函数交点坐标为(0.35,5.25).
则准点到校时间为7小时,0.35×60=21分.
故选A.
点评:本题考查了函数的图象,读懂函数图象的意义以及熟悉待定系数法求函数解析式是解题的关键.

练习册系列答案
相关题目
 某学生每天早晨骑自行车上学,早晨7点准时出发,以某一速度匀速前进.一天早上,由于有事,停下耽误了几分钟为了按时到校,他加快了速度,仍匀速前进,结果准点到校.这位同学这天早上7点出发的路程S(千米)与时间t(小时)的函数图象如图所示,则这位同学准点到校的时间为( )
某学生每天早晨骑自行车上学,早晨7点准时出发,以某一速度匀速前进.一天早上,由于有事,停下耽误了几分钟为了按时到校,他加快了速度,仍匀速前进,结果准点到校.这位同学这天早上7点出发的路程S(千米)与时间t(小时)的函数图象如图所示,则这位同学准点到校的时间为( )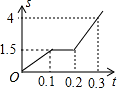 某学生每天早晨骑自行车上学,早晨7点准时出发,以某一速度匀速前进.一天早上,由于有事,停下耽误了几分钟为了按时到校,他加快了速度,仍匀速前进,结果准点到校.这位同学这天早上7点出发的路程S(千米)与时间t(小时)的函数图象如图所示,则这位同学准点到校的时间为
某学生每天早晨骑自行车上学,早晨7点准时出发,以某一速度匀速前进.一天早上,由于有事,停下耽误了几分钟为了按时到校,他加快了速度,仍匀速前进,结果准点到校.这位同学这天早上7点出发的路程S(千米)与时间t(小时)的函数图象如图所示,则这位同学准点到校的时间为