��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=a��x-2��2-2��y�ύ�ڵ�A��0��1����ֱ��AB��x�ύ�������ڵ�B����P��ֱ��AB��һ�㣨����A��B�غϣ���PQ��y�ύ�������ڵ�Q����PQΪб������������ֱ��������PQM�����P�ĺ�����Ϊm��
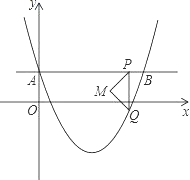
��1������������������Ӧ�ĺ�������ʽ��
��2�����߶�PQ��x��ƽ��ʱ����m��ֵ��
��3��������ֱ��������PQM����x����ֱ��AB֮���ͼ��Ϊ��Գ�������ʱ����m��ȡֵ��Χ��
��4��ֱ��д��������ֱ��������PQM������ֱ�DZ���������������������ʱm��ȡֵ��Χ��
���𰸡���1��y=![]() ��x-2��2-2����2��m1=2+
��x-2��2-2����2��m1=2+![]() ��m2=2-
��m2=2-![]() ����3��0��m��2-
����3��0��m��2-![]() ��2-
��2-![]() ��m��2+
��m��2+![]() ��2+
��2+![]() ��m��4����4��0��m��
��m��4����4��0��m��![]() ��m��
��m��![]() ��
��
��������
�����������1����A������������ʽֱ�����a��
��2����P��Q����x��Գƣ��Һ�������ͬ�����Q�����꣬���������߽���ʽ�У�����ֱ�����m��ֵ��
��3���ҵ������ٽ�㣺��Q��պ���x����ʱ����M��պ���x����ʱ�������������ٽ�״̬ʱ��mֵ������ȷ������Ҫ���m��ȡֵ��Χ��
��4������ֱ��������PQM������ֱ�DZ��������������������㣬Ҳ����y��ͬʱ����ֱ�DZ��ཻ������ֻ�����M��ǡ����y���ϵ��ٽ�״̬ʱ��mֵ���ɣ�
�����������1����A��0��1������y=a��x-2��2-2����1=a��0-2��2-2��
��a=![]() ��
��
��y=![]() ��x-2��2-2��
��x-2��2-2��
��2����Q��m��-1����
��-1=![]() ��m-2��2-2��
��m-2��2-2��
��m1=2+![]() ��m2=2-
��m2=2-![]() ��
��
��3������Q����x����ʱ��PQ=1��
��1-[![]() ��m-2��2-2]=1��
��m-2��2-2]=1��
��m1=2-![]() ��m2=2+
��m2=2+![]() ��
��
�൱0��m��2-![]() ��2-
��2-![]() ��m��2+
��m��2+![]() ��2+
��2+![]() ��m��4��Ϊ��Գ������Σ�
��m��4��Ϊ��Գ������Σ�
��4����M��պ���y����ʱ��|1-[![]() ��m-2��2-2]|=m��
��m-2��2-2]|=m��
��ã�m=![]() ��m=
��m=![]() ��
��
��0��m��![]() ��m��
��m��![]() ��
��

 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�