Question

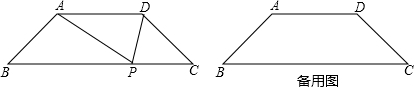
（2013•福州）如图，等腰梯形ABCD中，AD∥BC，∠B=45°，P是BC边上一点，△PAD的面积为

1

2

，设AB=x，AD=y
（1）求y与x的函数关系式；
（2）若∠APD=45°，当y=1时，求PB•PC的值；
（3）若∠APD=90°，求y的最小值．

Answer 1

分析：（1）如图1，过A作AE垂直于BC，在直角三角形ABE中，由∠B=45°，AB=x，利用锐角三角函数定义表示出AE，三角形PAD的面积以AD为底，AE为高，利用三角形面积公式表示出，根据已知的面积即可列出y与x的函数关系式；
（2）根据∠APC=∠APD+∠CPD，以及∠APC为三角形ABP的外角，利用外角性质得到关系式，等量代换得到∠BAP=∠CPD，再由四边形ABCD为等腰梯形，得到一对底角相等及AB=CD，可得出三角形ABP与三角形PDC相似，由相似得比例，将CD换为AB，由y的值求出x的值，即为AB的值，即可求出PB•PC的值；
（3）取AD的中点F，过P作PH垂直于AD，由直角三角形PF大于等于PH，当PF=PH时，PF最小，此时F与H重合，由三角形APD为直角三角形，利用直角三角形斜边上的中线等于斜边的一半得到PF等于AD的一半，表示出PF即为PH，三角形APD面积以AD为底，PH为高，利用三角形面积公式表示出三角形APD面积，由已知的面积求出y的值，即为最小值．

解答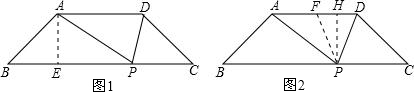：解：（1）如图1，过A作AE⊥BC于点E，
在Rt△ABE中，∠B=45°，AB=x，
∴AE=AB•sinB=

2

2

x，
∵S_△APD=

1

2

AD•AE=

1

2

，
∴

1

2

•y•

2

2

x=

1

2

，
则y=

2

x

；

（2）∵∠APC=∠APD+∠CPD=∠B+∠BAP，∠APD=∠B=45°，
∴∠BAP=∠CPD，
∵四边形ABCD为等腰梯形，
∴∠B=∠C，
∴△ABP∽△PCD，
∴

AB

PC

=

PB

DC

，
∴PB•PC=AB•DC=AB²，
当y=1时，x=

2

，即AB=

2

，
则PB•PC=（

2

）²=2；

（3）如图2，取AD的中点F，连接PF，
过P作PH⊥AD，可得PF≥PH，
当PF=PH时，PF有最小值，
∵∠APD=90°，
∴PF=

1

2

AD=

1

2

y，
∴PH=

1

2

y，
∵S_△APD=

1

2

•AD•PH=

1

2

，
∴

1

2

•y•

1

2

y=

1

2

，即y²=2，
∵y＞0，∴y=

2

，
则y的最小值为

2

．

点评：此题考查了相似形综合题，涉及的知识有：等腰梯形的性质，相似三角形的判定与性质，直角三角形斜边上的中线性质，以及三角形的面积求法，熟练掌握相似三角形的判定与性质是解本题的关键．