题目内容
如图,甲、乙两个可以自由转动的均匀的转盘,甲转盘被分成3个面积相等的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字,同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为m,乙转盘中指针所指区域内的数字为n(若指针指在边界线上时,重转一次,直到指针都指向一个区域为止).
【小题1】请你用画树状图或列表格的方法求出|m+n|>1的概率;
【小题2】直接写出点(m,n)落在函数y=-图象上的概率.
【小题1】表格如下:
(6分) 转盘乙 -1 0 1 2 转盘甲 -1 (-1,-1) (-1,0) (-1,1) (-1,2) -2 (-2,-1) (-2,0) (-2,1) (-2,2) 1 (1,-1) (1,0) (1,1) (1,2)
由表格可知,所有等可能的结果有12种,其中|m+n|>1的情况有5种,(7分)
所以|m+n|>1的概率为P1= ;(8分)
;(8分)
【小题2】点(m,n)在函数y=- 上的概率为P2=
上的概率为P2= =
= .(10分)
.(10分)
解析

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 所指区域内的数字为n(若指针指在边界线上时,重转一次,直到指针都指向一个区域为止).
所指区域内的数字为n(若指针指在边界线上时,重转一次,直到指针都指向一个区域为止).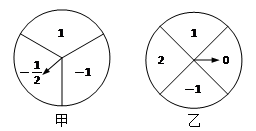
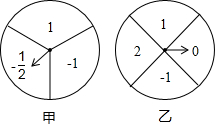
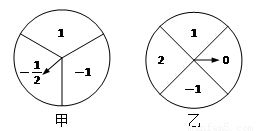
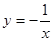 图象上的概率.
图象上的概率.