题目内容
16.已知二次函数y=$\frac{1}{2}$x2-4x+3.(1)求该二次函数图象的顶点坐标;
(2)当该二次函数的值为-3时,求自变量x的值.
分析 (1)利用配方法将y=x2-4x+3进行配方得出顶点形式,即可得出顶点坐标.
(2)把函数值代入解析式,解方程即可求得.
解答 解:(1)y=$\frac{1}{2}$x2-4x+3,
=$\frac{1}{2}$(x2-8x+16-16)+3,
=$\frac{1}{2}$(x-4)2-5,
∴二次函数图象的顶点坐标是:(4,-5);
(2)把y=-3代入y=$\frac{1}{2}$x2-4x+3得,-3=$\frac{1}{2}$x2-4x+3,
整理得,x2-8x+12=0,
解得x=2或6.
点评 本题考查了二次函数的性质,解答本题的关键是掌握二次函数的性质以及解二元一次方程的知识,此题难度不大.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
4.下列说法正确的是( )
| A. | 3x2-2x+5的项是3x,2x,5 | |
| B. | $\frac{x}{3}$-$\frac{y}{3}$与2x2-2xy-5都是多项式 | |
| C. | 多项式-2x2+4xy的次数是3 | |
| D. | 一个多项式的次数是6,则这个多项式中只有一项的次数是6 |
 如图,已知直线l:y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴交于点A,与y轴交于点B,将△AOB沿直线l折叠,点O落在点C处,求直线CA的表达式.
如图,已知直线l:y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴交于点A,与y轴交于点B,将△AOB沿直线l折叠,点O落在点C处,求直线CA的表达式.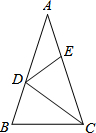 如图,在△ABC中,∠A=36°,AB=AC,CD是△ABC的角平分线.若在边AC上截取CE=CB,连接DE,则图中等腰三角形共有( )
如图,在△ABC中,∠A=36°,AB=AC,CD是△ABC的角平分线.若在边AC上截取CE=CB,连接DE,则图中等腰三角形共有( )