题目内容
【题目】已知![]() 是边长为4的等边三角形,点D是射线BC上的动点,将AD绕点A逆时针方向旋转
是边长为4的等边三角形,点D是射线BC上的动点,将AD绕点A逆时针方向旋转![]() 得到AE,连接DE.
得到AE,连接DE.
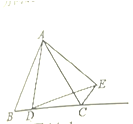
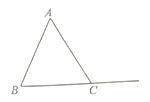
(1).如图,猜想![]() 是_______三角形;(直接写出结果)
是_______三角形;(直接写出结果)
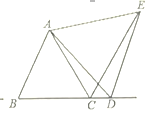
(2).如图,猜想线段CA、CE、CD之间的数量关系,并证明你的结论;
(3).①当BD=___________时,![]() ;(直接写出结果)
;(直接写出结果)
②点D在运动过程中,![]() 的周长是否存在最小值?若存在.请直接写出
的周长是否存在最小值?若存在.请直接写出![]() 周长的最小值;若不存在,请说明理由.
周长的最小值;若不存在,请说明理由.
【答案】(1)等边三角形;(2)![]() ,证明见解析;(3)①
,证明见解析;(3)①![]() 为
为![]() 或
或![]() 时,
时,![]() ;②最小值为
;②最小值为![]() ,理由见解析
,理由见解析
【解析】
(1)根据旋转的性质得到![]() ,根据等边三角形的判定定理解答;
,根据等边三角形的判定定理解答;
(2)证明![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,结合图形计算即可;
,结合图形计算即可;
(3)①分点![]() 在线段
在线段![]() 上和点
上和点![]() 在线段
在线段![]() 的延长线上两种情况,根据直角三角形的性质解答;②根据
的延长线上两种情况,根据直角三角形的性质解答;②根据![]() 得到
得到![]() ,根据垂线段最短解答.
,根据垂线段最短解答.
解:(1)由旋转变换的性质可知,![]() ,
,
![]() 是等边三角形,
是等边三角形,
故答案为:等边三角形;
(2)![]() ,
,
证明:由旋转的性质可知,![]() ,
,
![]() 是等边三角形
是等边三角形
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,
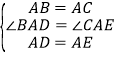 ,
,
![]()
![]() ,
,
![]() ;
;
(3)①![]() 为
为![]() 或
或![]() 时,
时,![]() ,
,
当点![]() 在线段
在线段![]() 上时,
上时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为
为![]() 或
或![]() 时,
时,![]() ;
;
②点![]() 在运动过程中,
在运动过程中,![]() 的周长存在最小值,最小值为
的周长存在最小值,最小值为![]() ,
,
理由如下:![]() ,
,
![]() ,
,
则![]() 的周长
的周长![]() ,
,
当![]() 最小时,
最小时,![]() 的周长最小,
的周长最小,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() 的最小值为
的最小值为![]() ,
,
![]() 的周长的最小值为
的周长的最小值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目