题目内容
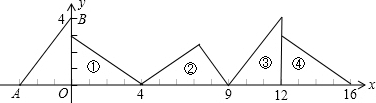
如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△AOB连续作旋转变换,依次得到三角形①、②、③、④、…,则三角形 的直角顶点的坐标为 .
的直角顶点的坐标为 .
 的直角顶点的坐标为
的直角顶点的坐标为
考点:坐标与图形变化-旋转
专题:规律型
分析:先根据勾股定理计算出AB=5,再计算出三角形②的直角顶点坐标为(7.2,2.4),每3个变换作为一个循环,每个循环直角顶点的横坐标增加12,由于32=3×10+2,则要进行10次循环,所以三角形 的直角顶点坐标与第②个三角形的直角顶点的纵坐标相同,横坐标为12×10+7.2.
的直角顶点坐标与第②个三角形的直角顶点的纵坐标相同,横坐标为12×10+7.2.
 的直角顶点坐标与第②个三角形的直角顶点的纵坐标相同,横坐标为12×10+7.2.
的直角顶点坐标与第②个三角形的直角顶点的纵坐标相同,横坐标为12×10+7.2.解答: 解:如图,作PH⊥x轴于H,
解:如图,作PH⊥x轴于H,
∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∴AB=
=5,
∵
PH•MN=
PM•PN,
∴PH=
=
=2.4,
∴MH=
=3.2,
∴三角形②的直角顶点坐标为(7.2,2.4),
∴△AOB连续3次作旋转变换,直角顶点的横坐标增加3+4+5=12,
而32=3×10+2,
∴三角形 的直角顶点坐标与第②个三角形的直角顶点的纵坐标相同,横坐标为12×10+7.2=127.2,
的直角顶点坐标与第②个三角形的直角顶点的纵坐标相同,横坐标为12×10+7.2=127.2,
即三角形 的直角顶点的坐标为(127.2,2.4).
的直角顶点的坐标为(127.2,2.4).
故答案为(127.2,2.4).
 解:如图,作PH⊥x轴于H,
解:如图,作PH⊥x轴于H,∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∴AB=
| OA2+OB2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴PH=
| 3×4 |
| 5 |
| 12 |
| 5 |
∴MH=
| PM2-PH2 |
∴三角形②的直角顶点坐标为(7.2,2.4),
∴△AOB连续3次作旋转变换,直角顶点的横坐标增加3+4+5=12,
而32=3×10+2,
∴三角形
 的直角顶点坐标与第②个三角形的直角顶点的纵坐标相同,横坐标为12×10+7.2=127.2,
的直角顶点坐标与第②个三角形的直角顶点的纵坐标相同,横坐标为12×10+7.2=127.2,即三角形
 的直角顶点的坐标为(127.2,2.4).
的直角顶点的坐标为(127.2,2.4).故答案为(127.2,2.4).
点评:本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
按如图规律摆放三角形,则第8堆三角形的个数为( )

| A、25个 | B、20个 |
| C、23个 | D、26个 |
 如图,矩形ABCD中AB=6cm,E为对角线BD上一点,EF⊥BC于F,若S△BEF:S四边形EFCD=1:3,则EF=
如图,矩形ABCD中AB=6cm,E为对角线BD上一点,EF⊥BC于F,若S△BEF:S四边形EFCD=1:3,则EF= 如图,在平行四边形ABCD中,已知AB=5cm,AC=12cm,BD=6cm,则△AOB的周长为
如图,在平行四边形ABCD中,已知AB=5cm,AC=12cm,BD=6cm,则△AOB的周长为 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=23度,那么∠2=
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=23度,那么∠2=