题目内容
已知x，y，z满足|x-2-z|+（3x-6y-7）2+|3y+3z-4|=0．求x，y，z的值．
解：根据非负数的性质，得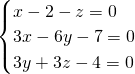
①×3+③，得3x+3y-10=0④
④-③，得y=
，
把y=代入④得x=3，
把x=3代入①得z=1．
∴原方程的解为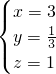
．
故x=3，y=，z=1．
分析：已知等式为三个非负数的和为0的形式，只有这几个非负数都为0，可组成方程组，求x、y、z的值．
点评：本题是方程组的运用，根据已知等式的特点，结合非负数的性质，组成方程组求解．
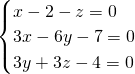
①×3+③，得3x+3y-10=0④
④-③，得y=
，把y=
代入④得x=3，把x=3代入①得z=1．
∴原方程的解为
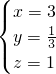．故x=3，y=
，z=1．分析：已知等式为三个非负数的和为0的形式，只有这几个非负数都为0，可组成方程组，求x、y、z的值．
点评：本题是方程组的运用，根据已知等式的特点，结合非负数的性质，组成方程组求解．
练习册系列答案
相关题目