题目内容
 如图所示,△ABC中,AH⊥BC于H,E,D,F分别是AB,BC,AC的中点,则四边形EDHF是( )
如图所示,△ABC中,AH⊥BC于H,E,D,F分别是AB,BC,AC的中点,则四边形EDHF是( )| A、一般梯形 | B、等腰梯形 | C、直角梯形 | D、直角等腰梯形 |
分析:根据三角形中位线定理及直角三角形中斜边上的中线为斜边的一半即可证明;
解答:解:在△ABC中,E,F分别是AB,AC的中点,∴EF=
BC,∴EF∥BC,
又∵E,D分别是AB,BC的中点,∴ED=
AC,
∵AH⊥BC,F是AC的中点,∴HF=
AC,
∴ED=HF,
∵EF∥DH,ED=HF且ED不平行HF,
∴四边形EDHF是等腰梯形,
故选B.
| 1 |
| 2 |
又∵E,D分别是AB,BC的中点,∴ED=
| 1 |
| 2 |
∵AH⊥BC,F是AC的中点,∴HF=
| 1 |
| 2 |
∴ED=HF,
∵EF∥DH,ED=HF且ED不平行HF,
∴四边形EDHF是等腰梯形,
故选B.
点评:本题考查了等腰梯形的判定及三角形中位线定理,属于基础题,关键是掌握直角三角形中斜边上的中线为斜边的一半.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
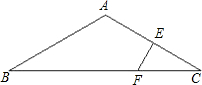 如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF. 16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=
16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=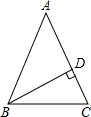 如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长.
如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长. 如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是
如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是 如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.
如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.