题目内容
探索研究
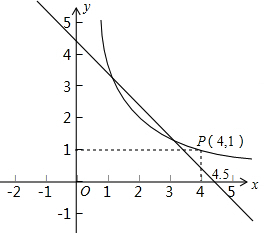
如图，在直角坐标系
中，点
为函数
在第一象限内的图象上的任一点，点
的坐标为
，直线
过
且与
轴平行，过作
轴的平行线分别交轴，于
，连结
交轴于
，直线
交轴于
．
（1）求证：点为线段的中点；
（2）求证：①四边形
为平行四边形；
②平行四边形为菱形；
（3）除点外，直线与抛物线有无其它公共点？并说明理由．
（1）法一：由题可知
．
，
，
．
，即为的中点．
法二：
，，
又
轴，
．
（2）①由（1）可知
，
，
，
，
．
，
又
，
四边形为平行四边形
②设
，
轴，则
，则
．
过作
轴，垂足为
，在
中，
．
平行四边形为菱形
（3）设直线
为
，由
，得
，代入得：
直线为
．
设直线与抛物线的公共点为
，代入直线关系式得：
，
，解得
．得公共点为
．
所以直线与抛物线只有一个公共点．
练习册系列答案
相关题目
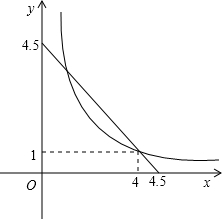由题意得方程组：
（2012•西城区模拟）探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”
中，点P为函数
在第一象限内的图象上的任一点，点A的坐标为
，直线
过
且与x轴平行，过
作y轴的平行线分别交x轴，
于
，连结
交x轴于H，直线
交y轴于R．
的中点；
为平行四边形； ②平行四边形
为菱形；
有无其它公共点？并说明理由． 