题目内容
已知:直线l1、l2分别与x轴交于点A、C,且都经过y轴上一点B,又l1的解析式是y=-x-3,l2与x轴正半轴的夹角是60°.求:(1)直线l2的函数表达式;
(2)△ABC的面积.
分析:(1)根据直线y=-x-3和x,y都有交点,求出A,B两点的坐标,根据直角三角函数,可得OC=
,得出C点坐标,根据B,C两点的坐标,很容易就可得到l2的函数表达式.
(2)根据A,B,C三点的坐标,可以得到高OB,底边AC的长度,根据三角形的面积公式可得△ABC的面积.
| 3 |
(2)根据A,B,C三点的坐标,可以得到高OB,底边AC的长度,根据三角形的面积公式可得△ABC的面积.
解答: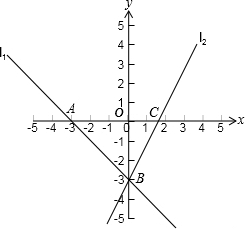 解:(1)∵?1:y=-x-3?2与y轴交于同一点B
解:(1)∵?1:y=-x-3?2与y轴交于同一点B
∴B(0,-3)又∵?2与x轴正半轴的夹角是60°
∴∠MCx=60°即∠OCB=60°
在Rt△BOC中OB=3∴OC=B•tan30°=3×
=
∴C(
,0)
令?:y=kx-3∴0=
k-3k=
∴y=
x-3
(2)又∵?1与x轴交于A,∴对于y=-x-3中当y=0时x=-3∴A(-3,0)
∴AC=
-(-3)=3+
∴S△ABC=
•(3+
)×3=
 解:(1)∵?1:y=-x-3?2与y轴交于同一点B
解:(1)∵?1:y=-x-3?2与y轴交于同一点B∴B(0,-3)又∵?2与x轴正半轴的夹角是60°
∴∠MCx=60°即∠OCB=60°
在Rt△BOC中OB=3∴OC=B•tan30°=3×
| ||
| 3 |
| 3 |
∴C(
| 3 |
令?:y=kx-3∴0=
| 3 |
| 3 |
∴y=
| 3 |
(2)又∵?1与x轴交于A,∴对于y=-x-3中当y=0时x=-3∴A(-3,0)
∴AC=
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
9+3
| ||
| 2 |
点评:本题要注意利用一次函数的特点,来列出方程,求出未知数,列出解析式,认真体会题意,画出图形;很容易就可看出数与图形的关系,很快即可得出结果

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 已知两直线l1和l2相交于点A(2,1),且直线l2经过坐标原点,若OA=OB
已知两直线l1和l2相交于点A(2,1),且直线l2经过坐标原点,若OA=OB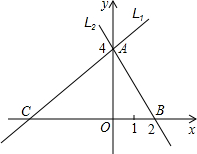 B两点,两直线相交于点A.
B两点,两直线相交于点A. (2012•成华区一模)已知两直线l1、l2分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.
(2012•成华区一模)已知两直线l1、l2分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示. 已知两直线L1和L2,直线L1的解析式是y=x-4,且直线L1与x轴交于点C,直线L2经过A、B两点,两直线相交于点A.
已知两直线L1和L2,直线L1的解析式是y=x-4,且直线L1与x轴交于点C,直线L2经过A、B两点,两直线相交于点A.