题目内容
如图，已知
=
=
，试说明：∠ABD=∠EBC．
证明：∵==，
∴△ABC∽△DBE（三边对应相等的两个三角形相似），
∴∠ABC=∠DBE，
∴∠ABC-∠DBC=∠DBE-∠DBC（等式的基本性质），
∴∠ABD=∠EBC．
分析：由==，可得△ABC∽△DBE，从而得出∠ABC=∠DBE，即可得出∠ABD=∠EBC．
点评：本题考查了相似三角形的判定和性质，主要考查了三边对应相等的两个三角形相似这个知识点．
==，∴△ABC∽△DBE（三边对应相等的两个三角形相似），
∴∠ABC=∠DBE，
∴∠ABC-∠DBC=∠DBE-∠DBC（等式的基本性质），
∴∠ABD=∠EBC．
分析：由
==，可得△ABC∽△DBE，从而得出∠ABC=∠DBE，即可得出∠ABD=∠EBC．点评：本题考查了相似三角形的判定和性质，主要考查了三边对应相等的两个三角形相似这个知识点．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
26、如图，已知直线l1∥l2，且l3和l1、l2分别交于A、B两点，点P在AB上．
15、如图，已知△ABC，点D在BC边上，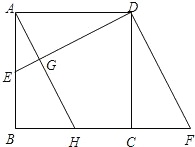
如图，已知正方形ABCD的边长是2，E是AB的中点，△ADE经逆时针旋转后与△CDF重合．
（2012•大港区一模）如图，已知反比例函数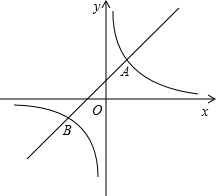
如图，已知反比例函数