题目内容
若△ABC的边长为a、b、c,且满足a2+b2+c2=ab+bc+ca,则△ABC的形状是( )
| A.等腰三角形 | B.等边三角形 | C.任意三角形 | D.不能确定 |
∵a2+b2+c2=ab+bc+ca,
∴2a2+2b2+2c2-2ab-2bc-2ca=0,
(a-b)2+(a-c)2+(b-c)2=0,
∴a=b=c,
∴三角形是等边三角形.
故选B.
∴2a2+2b2+2c2-2ab-2bc-2ca=0,
(a-b)2+(a-c)2+(b-c)2=0,
∴a=b=c,
∴三角形是等边三角形.
故选B.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目

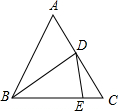 如图,△ABC为等边三角形,D,E分别是边AC,BC上的点(不与顶点重合),∠BDE=60°,若△ABC的边长为6,设DC=x,BE=y,则y与x之间的函数关系式是( )
如图,△ABC为等边三角形,D,E分别是边AC,BC上的点(不与顶点重合),∠BDE=60°,若△ABC的边长为6,设DC=x,BE=y,则y与x之间的函数关系式是( )
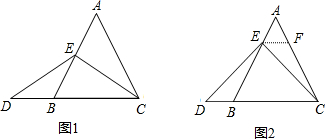
 如图,△ABC是等边三角形,D为AB边上的一个动点,DE∥BC,延长BC到F,使CF=AD,连接DF交AC于P.
如图,△ABC是等边三角形,D为AB边上的一个动点,DE∥BC,延长BC到F,使CF=AD,连接DF交AC于P.