题目内容
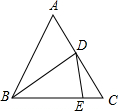 如图,△ABC为等边三角形,D,E分别是边AC,BC上的点(不与顶点重合),∠BDE=60°,若△ABC的边长为6,设DC=x,BE=y,则y与x之间的函数关系式是( )
如图,△ABC为等边三角形,D,E分别是边AC,BC上的点(不与顶点重合),∠BDE=60°,若△ABC的边长为6,设DC=x,BE=y,则y与x之间的函数关系式是( )分析:由△ABC为正三角形,推出∠A=∠C,∠3+∠1=120°,再由∠BDE=60°,推出∠3+∠2=120°,求得∠1=∠2,即可推出△DEC∽△BDA;由相似三角形的性质推出比例式
=
,然后根据图形推出AD=AC-CD,EC=BC-BE,根据正三角形的边长为6,并设DC=x,BE=y,即可推出y与x之间的函数关系式.
| CD |
| AB |
| EC |
| AD |
解答: 解:∵△ABC为正三角形,
解:∵△ABC为正三角形,
∴∠A=∠C=∠ABC=60°,
∴∠3+∠1=120°,
∵∠BDE=60°,
∴∠3+∠2=120°,
∴∠1=∠2,
∴△DEC∽△BDA,
∴
=
.
∵正△ABC的边长为6,
∴AB=BC=AC=6,
∵DC=x,BE=y,
∴
=
,即y=
x2-x+6.
故选C.
 解:∵△ABC为正三角形,
解:∵△ABC为正三角形,∴∠A=∠C=∠ABC=60°,
∴∠3+∠1=120°,
∵∠BDE=60°,
∴∠3+∠2=120°,
∴∠1=∠2,
∴△DEC∽△BDA,
∴
| CD |
| AB |
| EC |
| AD |
∵正△ABC的边长为6,
∴AB=BC=AC=6,
∵DC=x,BE=y,
∴
| x |
| 6 |
| 6-y |
| 6-x |
| 1 |
| 6 |
故选C.
点评:本题主要考查等边三角形的性质,平角的定义,相似三角形的判定与性质,关键在于通过对应角相等推出相关的三角形相似,正确地求出关于x与y的比例式,认真地进行计算.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=
16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=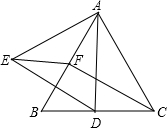 如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE. 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1 如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为一边作等边三角形ADE.
如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为一边作等边三角形ADE. 如图,△ABC为等边△,EC=ED,∠CED=120゜,P为BD的中点,求证:AE=2PE.
如图,△ABC为等边△,EC=ED,∠CED=120゜,P为BD的中点,求证:AE=2PE.