题目内容
如图,在边长为1的正方形网格内,点A、B、C、D、E均在格点处.请你判断∠x+∠y的度数,并加以证明.
答:∠x+∠y=45°. ……………………………………1分
证明:如图,以AG所在直线为对称轴,作AC的轴对称图 形AF,连结BF,
∵网格中的小正方形边长为1,且A、B、F均在格点处,
∴AB=BF=,AF=
.
∴
∴△ABF为等腰直角三角形,且∠ABF=90°. …………………2分
∴∠BAF=∠BFA=45°.
∵AF与AC关于直线AG轴对称,
∴∠FAG=∠CAG.
又∵AG∥EC,
∴∠x=∠CAG.
∴∠x=∠FAG. ………………………………………………………3分
∵DB∥AG,
∴∠y=∠BAG. ………………………………………………………4分
∴∠x+∠y=∠FAG+∠BAG =45°. ………………………………5分
解析:略

练习册系列答案
相关题目
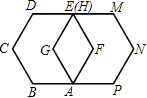 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( ) 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心, 长为半径作
长为半径作 ,
, ,
,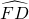 ,求阴影部分的面积.
,求阴影部分的面积. 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.