��Ŀ����
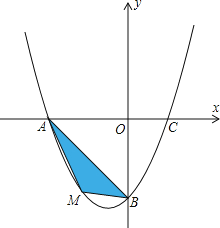
����Ŀ��˫ʮһ�ڼ䣬ij�ٻ��̳������ij��Ʒ����һ�δ����������Ʒ�Ľ���Ϊÿ��20Ԫ����֮ǰ�����۹����з��֣���ÿ���ۼ۶�Ϊ30Ԫʱ��ÿ��������Ϊ500�������ۼ�ÿ���1Ԫ��ÿ�µ�������������10����
��1�������Ʒ�ۼ����xԪʱ��ÿ�»�õ�����ΪyԪ����y����x�ĺ�������ʽ��
��2������̳���Ҫ��õ�������Ϊ8000Ԫ�������Ʒ�����۵���Ӧ��Ϊÿ������Ԫ��
��3�����й���۲��Ź涨������Ʒ�����۵��۲��ø�������۵����������ʱ�̳���õ�����������Ƕ��٣�
���𰸡���1��y����10x2+400x+5000��
��2��40Ԫ��60Ԫ��
��3��8000Ԫ��
��������
��1���������������������ϵ�����������������������������⣻
��2�����ݣ�1������õĺ�������ʽ������8000������һԪ���η��̼�����⣻
��3���������۵��۲��ø�������۵�����ȷ���Ա�����ȡֵ����������ֵ��
�⣺��1���������⣬��
y����30��20+x����500��10x��
����10x2+400x+5000��
��y����x�ĺ�������ʽΪy����10x2+400x+5000��
��2����y��8000ʱ��8000����10x2+400x+5000��
���x1��10��x2��30����30+x��40��60��
�𣺸���Ʒ�����۵���Ӧ��Ϊÿ��40Ԫ��60Ԫ��
��3��y����10x2+400x+5000��
����10��x��20��2+9000��
��Ϊ��Ʒ�����۵��۲��ø�������۵���������x![]()
���Ե�x��10�����ۼ�Ϊ40Ԫʱ��������������������Ϊ8000Ԫ��
�����������Ϊ8000Ԫ��

����Ŀ��2017����Ա�˫ʮһ������11������۶�ͻ��ʮ�ڣ�3�����ư��ڣ����ճɽ������1682��Ԫ�ϣ��ڽ����˫ʮһǰϦ��ij��ҵ����һ�ֱ�����Ʒ��Ϊ˫ʮһ��������Ʒ������֮ǰ�ij����г�������֣���Ʒ�����ܲ����ȶ���600������Ʒ����������a�������ɹ̶��������븡������������������ɣ����й̶����������ֲ��䣬�������������ۼ�x��Ԫ/������x��10���ɷ��ȣ��ҵõ������±����е���Ϣ��
�ۼ�x��Ԫ/���� | 5 | 8 |
��������Q������ | 580 | 400 |
��1����Q����x�ĺ�����ϵʽ��
��2����������������Ʒ���������꣬���ۼ�x��
��3�����ۼ�xΪ����ʱ�������۶������������ֵ��