Question

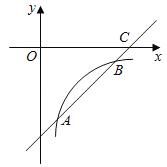
【题目】已知二次函数y=ax2+bx+（a＞0，b＜0）的图象与x轴只有一个公共点A

（1）当a=时，求点A的坐标；

（2）过点A的直线y=x+k与二次函数的图象相交于另一点B，当b≥﹣1时，求点B的横坐标m的取值范围

Answer 1

【答案】（1）A（1，0）；（2）m≥3．

【解析】

只有一个公共点A，则 再根据代入求出b.

构建方程组求出点B的横坐标，利用二次函数的性质即可解决问题；

解：（1）∵二次函数（a＞0，b＜0）的图象与x轴只有一个公共点A，

∵a=，

∴b2=1，

∵b＜0，

∴b=﹣1，

∴二次函数的解析式为

当y=0时， 解得x1=x2=1，

∴A（1，0）．

（2）∵b2=2a，

∴a=b2，

∴

当y=0时，,

∴A（，0），

将A代入y=x+k，得到k=，

由 ,

消去y得到：

解得

∵点A的横坐标为，

∴点B的横坐标m=，

∴

∵2＞0，

∴当时，m随的增大而减少，

∵﹣1≤b＜0，

∴≤﹣1，

∴

即m≥3．