题目内容
综合与探究
如图,抛物线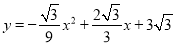 与
与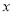 轴交于A、B两点(点A在点B的左侧),与
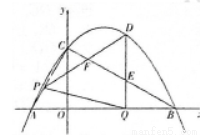
轴交于A、B两点(点A在点B的左侧),与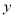 轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ,过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E.连接PD,与BC交于点F.设点P的运动时间为
轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ,过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E.连接PD,与BC交于点F.设点P的运动时间为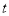 秒(
秒(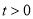 ).
).
(1)求直线BC的函数表达式.
(2)①直接写出P、D两点的坐标(用含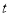 的代数式表示,结果需化简).
的代数式表示,结果需化简).
②在点P、Q运动的过程中,当PQ=PD时,求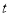 的值.
的值.
(3)试探究在点P、Q运动的过程中,是否存在某一时刻,使得点F为PD的中点.若存在,请直接写出此时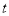 的值与点F的坐标;若不存在,请说明理由.
的值与点F的坐标;若不存在,请说明理由.
练习册系列答案
相关题目
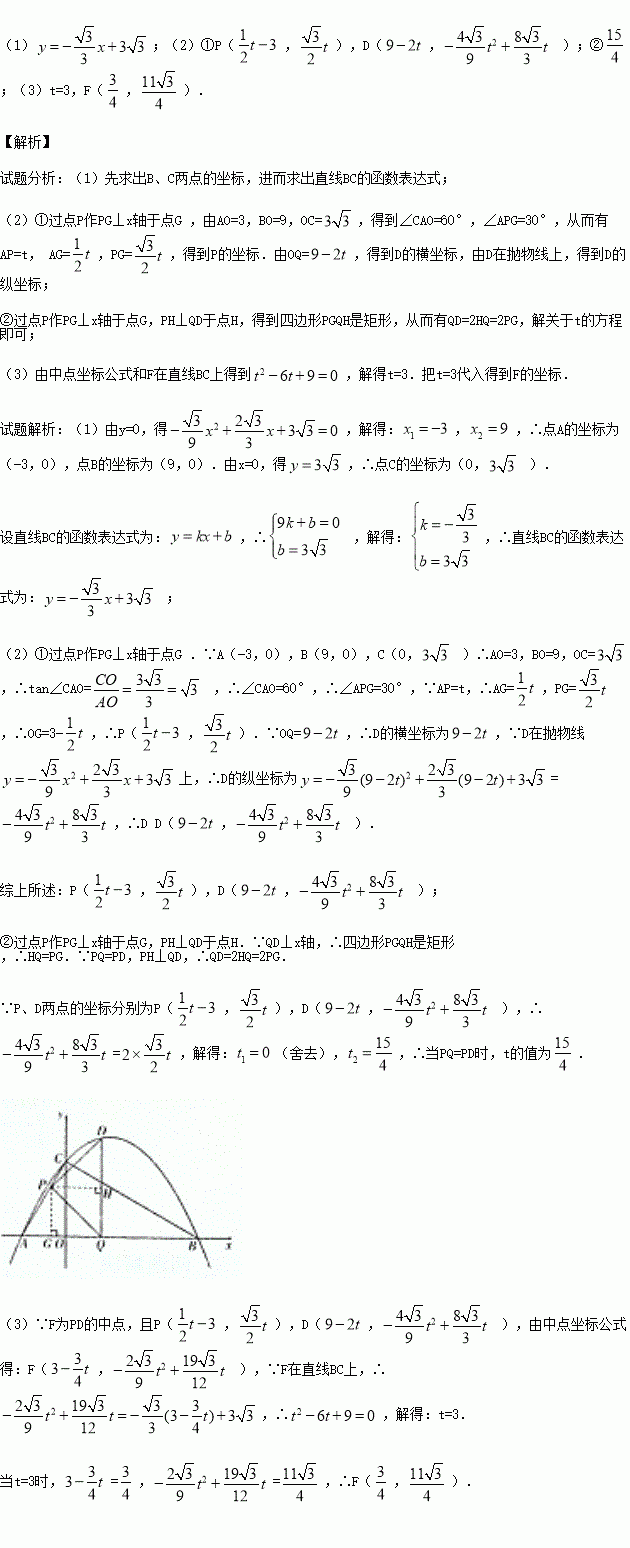

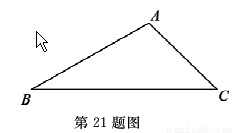
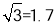 ,
,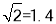 )
)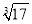 tan38°15′≈ .(结果精确到0.01)
tan38°15′≈ .(结果精确到0.01)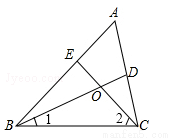
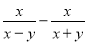 ,结果正确的是( )
,结果正确的是( )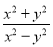 C.
C. 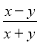 D.
D.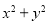
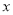 轴,
轴,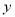 轴的正半轴上.函数
轴的正半轴上.函数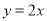 的图象与CB交于点D,函数
的图象与CB交于点D,函数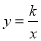 (
(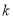 为常数,
为常数,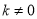 )的图象经过点D,与AB交于点E,与函数
)的图象经过点D,与AB交于点E,与函数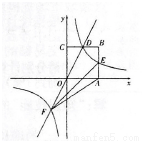
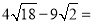 .
.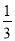 .
.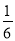 ;
;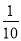 ;
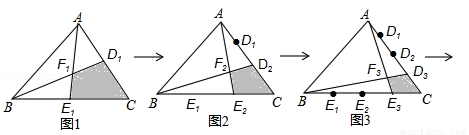
;
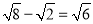 B.
B.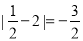
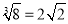 D.
D.