题目内容
当x=s-t与x=s+t时,二次函数y=x2-6x+1取值相等,则当x=s-1时,y=x2-6x+1的值是 .
考点:二次函数图象上点的坐标特征
专题:
分析:根据二次函数的对称性可知二次函数的对称轴为直线x=s,然后根据解析式求出s,再把x=s-1代入函数解析式计算即可得解.
解答:解:∵x=s-t与x=s+t时,二次函数y=x2-6x+1取值相等,
∴对称轴为直线x=s,
∴s=-
=3,
∴x=s-1=3-1=2,
y=22-6×2+1=4-12+1=-7.
故答案为:-7.
∴对称轴为直线x=s,
∴s=-
| -6 |
| 2×1 |
∴x=s-1=3-1=2,
y=22-6×2+1=4-12+1=-7.
故答案为:-7.
点评:本题考查了二次图象上点的坐标特征,利用二次函数的对称性求出对称轴然后求出s是解题的关键,也是本题的难点.

练习册系列答案
相关题目
下列各式中是二元一次方程的是( )
| A、y2-x=1 | ||||||
B、y+
| ||||||
C、
| ||||||
D、
|
 在一次“寻宝”游戏中,“寻宝”人找到了如图所标示的两个标志点A(2,3)、B(4,1),A、B两点到“宝藏”点的距离都是
在一次“寻宝”游戏中,“寻宝”人找到了如图所标示的两个标志点A(2,3)、B(4,1),A、B两点到“宝藏”点的距离都是| 10 |
| A、(1,0) |
| B、(5,4) |
| C、(1,0)或(5,4) |
| D、(0,1)或(4,5) |
下列图形中,既是轴对称图形又是中心对称图形的个数是( )


| A、1个 | B、2个 | C、3个 | D、4个 |
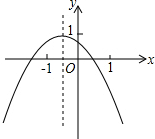 如图所示的二次函数图象,以下四个结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.你认为正确的有
如图所示的二次函数图象,以下四个结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.你认为正确的有