题目内容
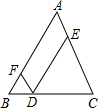如图所示，已知D是等腰三角形ABC底边BC上的一点，点E，F分别在AC，AB上，且DE∥AB，DF∥AC．求证：DE+DF=AB．分析：首先根据两组对边互相平行的四边形是平行四边形判定出四边形AEDF是平行四边形，进而得到DF=AE，然后证明DE=CE，即可得到DE+DF=AB．
解答：证明：∵DE∥AB，DF∥AC，
∴四边形AEDF是平行四边形，
∴DF=AE，
又∵DE∥AB，
∴∠B=∠EDC，
又∵AB=AC，
∴∠B=∠C，
∴∠C=∠EDC，
∴DE=CE，
∴DF+DE=AE+CE=AC=AB．
∴四边形AEDF是平行四边形，
∴DF=AE，
又∵DE∥AB，
∴∠B=∠EDC，
又∵AB=AC，
∴∠B=∠C，
∴∠C=∠EDC，
∴DE=CE，
∴DF+DE=AE+CE=AC=AB．
点评：此题主要考查了平行四边形的判定与性质，关键是掌握平行四边形对边平行且相等，两组对边分别平行的四边形是平行四边形．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
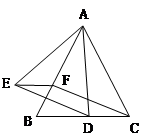
21、如图所示，已知△ABC是等边三角形，点D、B、C、E在同一条直线上，且∠DAE=120°．
