Question

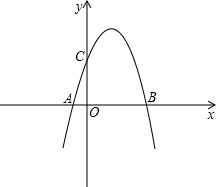抛物线与x轴交于A（-2，0），B（6，0），与y轴交于C（0，4），这个二次函数的解析式是

 

．

Answer 1

分析：已知函数经过A（-2，0），B（6，0），可设抛物线解析式的交点式，即y=a（x+2）（x-6），再把C（0，4）代入，可求a，从而确定抛物线解析式．

解答：解：根据已知A（-2，0），B（6，0）两点坐标，
可设函数的解析式y=a（x+2）（x-6），
把点C（0，4）坐标代入，得：
4=a×2×（-6），
解得a=-

1

3

，
∴函数解析式是y=-

1

3

（x+2）（x-6），
即y=-

1

3

x2+

4

3

x+4．

点评：当已知函数图象与x轴有两交点时，利用交点式求解析式比较简单；
当已知函数的顶点坐标，或已知函数对称轴时，利用顶点式求解析式比较简单；
当已知函数图象经过一般的三点时，利用一般式求解．