题目内容
由下列所给边长相同的正多边形的组合中,不能铺满地面的是
- A.正方形和正六边形
- B.正方形与正三角形
- C.正三角形与正六边形
- D.正三角形、正方形、正六边形
A
分析:正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
解答:A、正方形的每个内角是90°,正六边形的每个内角是120°,90m+120n=360°,m=4- n,显然n取任何整数时,m不能得正整数,故不能铺满,符合题意;
n,显然n取任何整数时,m不能得正整数,故不能铺满,符合题意;
B、正三角形的每个内角是60°,正方形的每个内角是90°,∵3×60°+2×90°=360°,∴能铺满地面,不符合题意;
C、正三角形的每个内角是60°,正六边形的每个内角是120度,∵2×60°+2×120°=360°,∴能铺满地面,不符合题意;
D、正三角形的每个内角是60°,正方形的每个内角是90°,正六边形的每个内角是120度,∵60°+2×90°+120°=360°,∴能铺满地面,不符合题意.
故选:A.
点评:本题考查平面镶嵌的知识.几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
分析:正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
解答:A、正方形的每个内角是90°,正六边形的每个内角是120°,90m+120n=360°,m=4-
 n,显然n取任何整数时,m不能得正整数,故不能铺满,符合题意;
n,显然n取任何整数时,m不能得正整数,故不能铺满,符合题意;B、正三角形的每个内角是60°,正方形的每个内角是90°,∵3×60°+2×90°=360°,∴能铺满地面,不符合题意;
C、正三角形的每个内角是60°,正六边形的每个内角是120度,∵2×60°+2×120°=360°,∴能铺满地面,不符合题意;
D、正三角形的每个内角是60°,正方形的每个内角是90°,正六边形的每个内角是120度,∵60°+2×90°+120°=360°,∴能铺满地面,不符合题意.
故选:A.
点评:本题考查平面镶嵌的知识.几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某瓜农采用大棚栽培技术种植了一亩地的良种西瓜,这亩地产西瓜600个,在西瓜上市前该瓜农随机摘下了10个成熟的西瓜,称重如下:
| 西瓜质量(单位:千克) | 5.4 | 5.3 | 5.0 | 4.8 | 4.4 | 4.0 |
| 西瓜数量(单位:个) | 1 | 2 | 3 | 2 | 1 | 1 |
(2)计算这10个西瓜的平均质量,并根据计算结果估计这亩地共可收获西瓜约多少千克?




 ,其中x=3.”
,其中x=3.” 如图,已知AB∥CD,∠E=80°,∠B=30°,则∠C=________.
如图,已知AB∥CD,∠E=80°,∠B=30°,则∠C=________. 是反比例函数,则m=________.
是反比例函数,则m=________. cm
cm cm
cm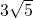 cm
cm cm
cm