题目内容
如图(1)在正方形ABCD中,对角线AC与BD相交于点E,AF平分于∠BAC,交BD于点F。

【小题1】求证:EF+- AC =AB
【小题2】点C1从C出发,沿着线段CB向点B运动(不与点B重合),同时点A1从A出发,沿着BA的延长线运动,点C1与点A1的运动速度相同,当运点C1停止运动时,另一动点A1也随之停止运动。如图(2)A1、F1平分∠BA∠BA1C1,交BD于F1,过点F1作F1E1⊥A1C1,垂足为E1,请猜想E1 F1, A1C1,与AB三者之间的数量关系,并证明你的猜想
A1C1,与AB三者之间的数量关系,并证明你的猜想
【小题3】在(2)的条件下,当A1E1=3,C1E1=2,求BD的长。
【小题1】过点F作FM⊥AB,RT△AMF≌△AEF ∴AM=AE ∵∠ABE=45°∴BM=MF ∴AB= EF+
EF+ AC
AC
【小题2】连接F1C1,过点F1作F1P⊥A1B于P,F1Q⊥BC于点Q
∵A1F平分∠BA1C1∴E1F1=PF1∴E1F1=PF1=QF1∵A1F=A1F∴RT△A1E1F1≌RT△A1PF1∴A1E1=A1P
同理QF1=PF1,∴E1F1=PF1=QF1∵A1F=A1F RT△A1E1F1≌RT△A1PF1∴A1E1=A1P同理RT△QF1C1≌RT△E1F1C1
C1Q=C1E1∵A1A=C1C∴A1B+BC1=AB+A1A+BC=2AB∴PB=PF1=QF1=QB
∴A1B+BC1=A1P+PB+QB+C1Q=A1P+C1Q+2E1F1
∴2AB=A1E1+C1E1+2E1F1=A1C1+2E1F1
∴E1F1+ A1C1=AB
A1C1=AB
【小题3】设PB=X∴QB="X "
∵A1E1=3;E1C1=2;A1P=A1E1=3;QC1=C1E1=2在RT△A1BC1中A1B +BC1
+BC1 =A1C1
=A1C1 即(3+X)
即(3+X) +(2+X)
+(2+X) =5
=5
∴X1=1,X2=-6(舍)∴PB=1,E1F1=1,∵A1C1=5∴AB= ,BD=
,BD=

解析

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案 如图所示,在正方形ABCD中,点E、F分别是AD、BC的中点.求证:四边形BFDE是平行四边形.
如图所示,在正方形ABCD中,点E、F分别是AD、BC的中点.求证:四边形BFDE是平行四边形.
 如图所示,在正方形ABCD中,P是AD边上一点,PH⊥AC,垂足为H,HC=CD,求∠HPC的度数.
如图所示,在正方形ABCD中,P是AD边上一点,PH⊥AC,垂足为H,HC=CD,求∠HPC的度数.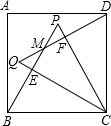 如图所示,在正方形ABCD中,△PCB和△QCD是正三角形,BP与QD相交于M,QC与PB相交于F,请你猜想QM与PM的大小关系?并证明你的猜想.
如图所示,在正方形ABCD中,△PCB和△QCD是正三角形,BP与QD相交于M,QC与PB相交于F,请你猜想QM与PM的大小关系?并证明你的猜想.