题目内容
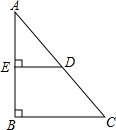如图示，在△ABC中，∠A=30°，∠C=60°，CD=1，DE垂直平分AB，分别交AC，AB于D，E，则AD=________．
1
分析：连接BD，根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，再根据等边对等角的性质可得∠ABD=∠A，然后求出∠CBD=60°，从而得到△BCD是等边三角形，根据等边三角形的三边都相等解答即可．
解答：
解：连接BD，∵DE垂直平分AB，
∴AD=BD，
∴∠ABD=∠A=30°，
∴∠CBD=90°-30°=60°，
∵∠C=60°，
∴△BCD是等边三角形，
∴BD=CD=1，
故AD=1．
故答案为：1．
点评：本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，等边三角形的判定与性质，作出辅助线是解题的关键．
分析：连接BD，根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，再根据等边对等角的性质可得∠ABD=∠A，然后求出∠CBD=60°，从而得到△BCD是等边三角形，根据等边三角形的三边都相等解答即可．
解答：
解：连接BD，∵DE垂直平分AB，∴AD=BD，
∴∠ABD=∠A=30°，
∴∠CBD=90°-30°=60°，
∵∠C=60°，
∴△BCD是等边三角形，
∴BD=CD=1，
故AD=1．
故答案为：1．
点评：本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，等边三角形的判定与性质，作出辅助线是解题的关键．
练习册系列答案
导学全程练创优训练系列答案
相关题目
湖州太湖边上有一座景观桥叫彩虹桥，桥洞形状如抛物线ABC，其横截面如图，在图中建立的直角坐标系中，抛物线的解析式为
如图示，在△ABC中，∠A=30°，∠C=60°，CD=1，DE垂直平分AB，分别交AC，AB于D，E，则AD=
已知：如图示，在Rt△ABC中，∠A=90°，∠ABC=2∠C，BD是∠ABC的平分线．求证：CD=2AD．