题目内容
一次函数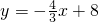 的图象与y轴、x轴围成的三角形的内切圆半径是________.
的图象与y轴、x轴围成的三角形的内切圆半径是________.
2
分析:求出一次函数与x、y轴的交点坐标,求出AB长,设三角形OAB的内切圆的圆心是I,半径是R,连接IA、IB、IO,根据三角形的面积公式得出△IAB、△IOA,△IOB的面积之和等于△OAB的面积,代入求出即可.
解答: 解:设一次函数与y轴交于A、与x轴交于B,
解:设一次函数与y轴交于A、与x轴交于B,
当x=0时,y=8,
∴OA=8,
当y=0时,0=- x+8,
x+8,
∴x=6,
∴OB=6,
在△AOB中,由勾股定理得:AB=10,
设三角形OAB的内切圆的圆心是I,半径是R,连接IA、IB、IO,
由三角形的面积公式得:S△IAO+S△IAB+S△IOB=S△AOB,
 ∴
∴ OA×OB=
OA×OB= OA×R+
OA×R+ OB×R+
OB×R+ AB×R,
AB×R,
∴6×8=6R+8R+10R,
∴R=2.
故答案为:2.
点评:本题考查了三角形的面积,一次函数图象上点的坐标特征,勾股定理等知识点的运用,主要考查学生解题的技巧,题目较好,具有一定的代表性.
分析:求出一次函数与x、y轴的交点坐标,求出AB长,设三角形OAB的内切圆的圆心是I,半径是R,连接IA、IB、IO,根据三角形的面积公式得出△IAB、△IOA,△IOB的面积之和等于△OAB的面积,代入求出即可.
解答:
 解:设一次函数与y轴交于A、与x轴交于B,
解:设一次函数与y轴交于A、与x轴交于B,当x=0时,y=8,
∴OA=8,
当y=0时,0=-
 x+8,
x+8,∴x=6,
∴OB=6,
在△AOB中,由勾股定理得:AB=10,
设三角形OAB的内切圆的圆心是I,半径是R,连接IA、IB、IO,
由三角形的面积公式得:S△IAO+S△IAB+S△IOB=S△AOB,
 ∴
∴ OA×OB=
OA×OB= OA×R+
OA×R+ OB×R+
OB×R+ AB×R,
AB×R,∴6×8=6R+8R+10R,
∴R=2.
故答案为:2.
点评:本题考查了三角形的面积,一次函数图象上点的坐标特征,勾股定理等知识点的运用,主要考查学生解题的技巧,题目较好,具有一定的代表性.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
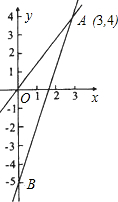 如图所示,一个正比例函数图象与一个一次函数图象交于点(3,4),且一次函数的图象与y轴相交于点B.
如图所示,一个正比例函数图象与一个一次函数图象交于点(3,4),且一次函数的图象与y轴相交于点B.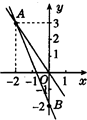 如图所示,一个正比例函数与一个一次函数的图象相交于点A(-2,3),且一次函数的图象与y轴相交于点B.
如图所示,一个正比例函数与一个一次函数的图象相交于点A(-2,3),且一次函数的图象与y轴相交于点B.