题目内容
如图所示，∠A=90°，BD是△ABC的角平分线，AC=8cm，DC：AD=3：1，则点D到BC的距离为________．
2cm
分析：过点D作DE⊥BC于E，根据角平分线上的点到角的两边的距离相等可得DE=AD，然后求出AD的长度即可得解．
解答：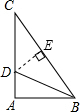
解：如图，过点D作DE⊥BC于E，
∵∠A=90°，BD是△ABC的角平分线，
∴DE=AD，
∵AC=8cm，DC：AD=3：1，
∴AD=8×
=2cm，
∴DE=2cm．
故答案为：2cm．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．
分析：过点D作DE⊥BC于E，根据角平分线上的点到角的两边的距离相等可得DE=AD，然后求出AD的长度即可得解．
解答：
解：如图，过点D作DE⊥BC于E，∵∠A=90°，BD是△ABC的角平分线，
∴DE=AD，
∵AC=8cm，DC：AD=3：1，
∴AD=8×
=2cm，∴DE=2cm．
故答案为：2cm．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．
练习册系列答案
相关题目
远处时，此水渠的造价最低，最低造价是多少？
22、如图所示，∠AOB=90°，OE、OF分别平分∠AOB、∠BOC，如果∠EOF=60°，求∠BOC的度数．
如图所示，∠ABC=90°，∠C=30°，BD⊥AC于D，AB=10，则BD的长为（ ）
观察、探究与思考：