题目内容
求抛物线y=-2（x+1）（x-3）的对称轴和顶点坐标．
解：令y=-2（x+1）（x-3）=0，
解得：x=-1，或x=3，
∴与x轴的交点坐标为：（-1，0）和（3，0）
∴对称轴为：x=
=1，
当x=1时，y=-2（1+1）（1-3）=8，
∴顶点坐标为（1，8）
分析：首先求得抛物线与x轴的交点坐标，然后求得其对称轴和顶点坐标即可．
点评：本题考查了二次函数的性质，解题时也可化为一般形式然后利用配方法求解．
解得：x=-1，或x=3，
∴与x轴的交点坐标为：（-1，0）和（3，0）
∴对称轴为：x=
=1，当x=1时，y=-2（1+1）（1-3）=8，
∴顶点坐标为（1，8）
分析：首先求得抛物线与x轴的交点坐标，然后求得其对称轴和顶点坐标即可．
点评：本题考查了二次函数的性质，解题时也可化为一般形式然后利用配方法求解．
练习册系列答案
相关题目
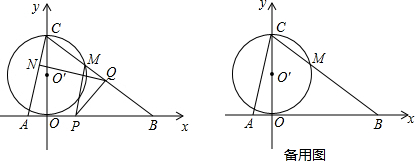
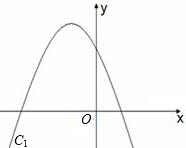已知抛物线C1与x轴的一个交点为交于（-4，0），对称轴为x=-1.5，并过点（-1，6），
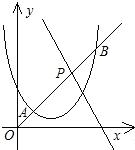已知抛物线y=x2-2x+6-m与直线y=-2x+6+m，它们的一个交点的纵坐标是4．
（2012•黔东南州）如图，已知抛物线经过点A（-1，0）、B（3，0）、C（0，3）三点．
（2011•荔湾区一模）抛物线y=-x2+（m-1）x+m与y轴交于（0，3）点．