Question

已知抛物线y=x²-2x+6-m与直线y=-2x+6+m，它们的一个交点的纵坐标是4．
（1）求抛物线和直线的解析式；
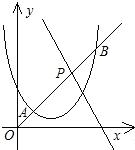
（2）如图，直线y=kx（k＞0）与（1）中的抛物线交于两个不同的点A、B，与（1）中的直线交于点P，试证明：

OP

PA

+

OP

OB

=2；
（3）在（2）中能否适当选取k值，使A、B两点的纵坐标之和等于8？如果能，求出此时的k值；如果不能请说明理由．

Answer 1

分析：（1）由抛物线与直线的纵坐标都是4，代入函数解析式，联立方程组解答即可；
（2）分别过A、P、B分别作x轴的垂线，利用平行线分线段成比例及根与系数的关系解决问题；
（3）假设k存在，与y=x²-2x+4联立方程，求得k的值，代入y=x²-2x+4验证即可解决问题．

解答：解：（1）由题意知x²-2x+6-m=4，-2x+6+m=4，
联立方程组解得m=2，
所以抛物线和直线的解析式分别为y=x²-2x+4，y=-2x+8；

（2）分别过A、P、B分别作x轴的垂线，垂足分别为A′、P′、B′，
则AA′∥PP′∥BB′，
由平行线分线段成比例定理有：

OP

OA

+

OP

OB

=

xP

xA

+

xP

xB

=

xP(xA+xB)

xA•xB

（1），
把y=kx（k＞0）代入抛物线y=x²-2x+4得x²-（2+k）x+4=0，
由韦达定理有：x_A+x_B=2+k，x_A•x_B=4（2），
把y=kx（k＞0）代入y=-2x+8中有：x_p=

8

k+2

（3），
将（2）（3）代入（1）式中有：

OP

OA

+

OP

OB

=

8

k+2

•

k+2

4

=2；

（3）假设k存在，则x²-2x+4=kx，即x²-（2+k）x+4=0，
x_A+x_B=2+k，故纵坐标之和为：k（k+2）=8
解得，k=-4或k=2，
当k=-4时与k＞0矛盾；
当k=2时，x_A=x_B与A、B是不同的两个交点矛盾；
故不存在这样的k值．

点评：此题主要待定系数法求函数解析式，平行线分线段成比例定理，根与系数的关系以及一次函数的交点问题．