题目内容
阅读以下材料并填空：平面上有n个点（n≥2）且任意三个点不在同一直线上，过这些点作直线一共能作出多少条不同的直线？分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线，当有5个点时可连成10条直线…推导：平面上有n个点，因为两点可确定一条直线，所以每个点都可与除本身之外的其余（n﹣1）个点确定一条直线，即共有n（n﹣1）条直线．但因AB与BA是同一条直线，故每一条直线都数了2遍，所以直线的实际总条数为
．
试结合以上信息，探究以下问题：平面上有n（n≥3）个点，任意3个点不在同一直线上，过任意3点作三角形，一共能作出多少个不同的三角形？
分析：考察点的个数n和可作出的三角形的个数 sn，发现：（填下表）
推到:
．试结合以上信息，探究以下问题：平面上有n（n≥3）个点，任意3个点不在同一直线上，过任意3点作三角形，一共能作出多少个不同的三角形？
分析：考察点的个数n和可作出的三角形的个数 sn，发现：（填下表）
推到:
解：顺次连接不在同一直线上的三个点可作1个三角形；当有4个点时，可作4个三角形；当有5个点时，可作10个三角形；
依次类推当有n个点时，可作
个三角形．
答案：1、4、10、
．
平面上有n个点，过不在同一直线上的三点可以确定1个三角形，取第一个点A有n种取法，取第二个点B有（n﹣1）种取法．取第三个点C有（n﹣2）种取法，
但△ABC、△ACB、△BAC、△BCA、△CAB、△CBA是同一个三角形，故应除以6，
即
．
依次类推当有n个点时，可作
个三角形．答案：1、4、10、
．平面上有n个点，过不在同一直线上的三点可以确定1个三角形，取第一个点A有n种取法，取第二个点B有（n﹣1）种取法．取第三个点C有（n﹣2）种取法，
但△ABC、△ACB、△BAC、△BCA、△CAB、△CBA是同一个三角形，故应除以6，
即
．
练习册系列答案
相关题目
阅读以下材料并填空．
平面上有n个点（n≥2），且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？
试探究以下问题：平面上有n（n≥3）个点，任意三个点不在同一直线上，过任意三点作三角形，一共能作出多少不同的三角形？
（1）分析：当仅有两个点时，可连成1条直线；当仅有3个点时，可作 条直线；当有4个点时，可作 条直线；当有5个点时，可作 条直线；
（2）归纳：考察点的个数n和可作出的直线的条数Sn，发现：（填下表）
（3）推理： ；
（4）结论： ．
平面上有n个点（n≥2），且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？
试探究以下问题：平面上有n（n≥3）个点，任意三个点不在同一直线上，过任意三点作三角形，一共能作出多少不同的三角形？
（1）分析：当仅有两个点时，可连成1条直线；当仅有3个点时，可作
（2）归纳：考察点的个数n和可作出的直线的条数Sn，发现：（填下表）
| 点的个数 | 可连成直线的条数 |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| … | |
| n |
（4）结论：
阅读以下材料并填空．
平面上有n个点（n≥2），且任意三个点不在同一直线上，过这些点作直线，一共能作出多少条不同的直线？
（1）分析：当仅有两个点时，可连成1条直线；
当有3个点时，可连成3条直线；
当有4个点时，可连成6条直线；
当有5个点时，可连成10条直线；
…
（2）归纳：考察点的个数n和可连成直线的条数Sn，发现：
（3）推理：平面上有n个点，两点确定一条直线．取第一个点A有n种取法，取第二个点B有（n-1）种取法，所以一共可连成n（n-1）条直线，但AB与BA是同一条直线，故应除以2，即Sn=
．
（4）结论：Sn=
．
试探究以下问题：
平面上有n（n≥3）个点，任意三个点不在同一直线上，过任意三点作三角形，一共能作出多少不同的三角形？
①分析：
当仅有3个点时，可作 个三角形；
当有4个点时，可作 个三角形；
当有5个点时，可作 个三角形；
…
②归纳：考察点的个数n和可作出的三角形的个数Sn，发现：
③推理：
取第一个点A有n种取法，
取第二个点B有（n-1）种取法，
取第三个点C有（n-2）种取法，
但△ABC、△ACB、△BAC、△BCA、△CAB、△CBA是同一个三角形，故应除以6．
④结论： ．
平面上有n个点（n≥2），且任意三个点不在同一直线上，过这些点作直线，一共能作出多少条不同的直线？
（1）分析：当仅有两个点时，可连成1条直线；
当有3个点时，可连成3条直线；
当有4个点时，可连成6条直线；
当有5个点时，可连成10条直线；
…
（2）归纳：考察点的个数n和可连成直线的条数Sn，发现：
（3）推理：平面上有n个点，两点确定一条直线．取第一个点A有n种取法，取第二个点B有（n-1）种取法，所以一共可连成n（n-1）条直线，但AB与BA是同一条直线，故应除以2，即Sn=
| n(n-1) |
| 2 |
（4）结论：Sn=
| n(n-1) |
| 2 |
| 点的个数 | 可连成直线条数 | ||
| 2 | l=S2=
| ||
| 3 | 3=S3=
| ||
| 4 | 6=S4=
| ||
| 5 | 10=S5=
| ||
| … | … | ||
| n | Sn=
|
平面上有n（n≥3）个点，任意三个点不在同一直线上，过任意三点作三角形，一共能作出多少不同的三角形？
①分析：
当仅有3个点时，可作
当有4个点时，可作
当有5个点时，可作
…
②归纳：考察点的个数n和可作出的三角形的个数Sn，发现：
| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| … | … |
| n |
取第一个点A有n种取法，
取第二个点B有（n-1）种取法，
取第三个点C有（n-2）种取法，
但△ABC、△ACB、△BAC、△BCA、△CAB、△CBA是同一个三角形，故应除以6．
④结论：
？
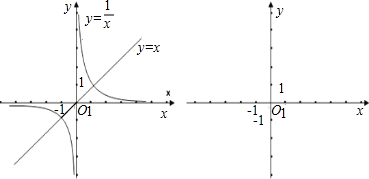
则在同一直角坐标系中画出这两个函数的草图．
，解得
或
∴两个图象的交点为（1，1）和（-1，-1）
（1）上述解题过程用的数学思想方法是______；
时，x的取值范围是______；
．（要求画出草图）