Question

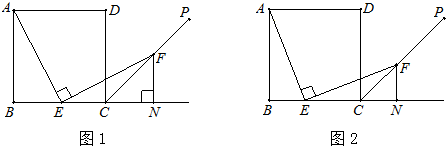
如图（图1，图2），四边形ABCD是边长为4的正方形，点E在线段BC上，∠AEF=90°，且EF交正方形外角平分线CP于点F，交BC的延长线于点N，FN⊥BC．
（1）若点E是BC的中点（如图1），AE与EF相等吗？
（2）点E在BC间运动时（如图2），设BE=x，△ECF的面积为y．
①求y与x的函数关系式；
②当x取何值时，y有最大值，并求出这个最大值．

Answer 1

分析：（1）在AB上取一点G，使AG=EC，连接GE，利用ASA，易证得：△AGE≌△ECF，则可证得：AE=EP；
（2）同（1）可证明AE=EF，利用AAS证明△ABE≌△ENF，根据全等三角形对应边相等可得FN=BE，再表示出EC，然后利用三角形的面积公式即可列式表示出△ECF的面积为y，然后整理再根据二次函数求解最值问题．

解答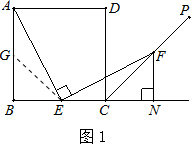：解：（1）在AB上取一点G，使AG=EC，连接GE．
∴AB-AG=BC-EC，
即BG=BE，
∴∠BGE=45°，
∴∠AGE=135°．
∵CP是外角平分线，
∴∠DCF=45°，
∴∠ECF=135°，
∴∠AGE=∠ECF，
∵∠AEB+∠BAE=90°，∠AEB+∠CEF=90°，
∠BAE=∠CEF，
在△AGE和△ECF中，

∠AGE=∠ECF AG=EC ∠BAE=∠CEF

，
∴△AGE≌△ECF（ASA），
∴AE=EF；

（2）①与（1）同理可证，当E不是中点时，AE=EF，
∴在△ABE和△ENF中，

∠BAE=∠CEF ∠B=∠CNF=90° AE=EF

，
∴△ABE≌△ENF（AAS），
∴FN=BE=x，
又∵BE=x，BC=4，
∴EC=4-x，
∴y=

1

2

×（4-x）x，
∴y=-

1

2

x²+2x （0＜x＜4），
②y=-

1

2

x²+2x=-

1

2

（x²-4x）=-

1

2

（x-2）²+2，
∴当x=2，y_最大值=2．

点评：本题考查了正方形的性质，全等三角形的判定与性质，二次函数的最值问题，综合性较强，准确作出辅助线是解题的关键．