题目内容
 如图,图1是一个正六边形,分别连接这个正六边形各边中点得到图2,再分别连接图2内小正六边形各边中点得到图3.
如图,图1是一个正六边形,分别连接这个正六边形各边中点得到图2,再分别连接图2内小正六边形各边中点得到图3.(1)填写下表:
| 图形标号 | 1 | 2 | 3 |
| 正六边形个数 | 1 | 2 | |
| 三角形个数 | 0 | 6 |
(3)某个图形中,能否分出2010个三角形?简述你的理由.
分析:(1)观察可得第3个图形中有3个正六边形,12个三角形;
(2)得到第n个图形中三角形的个数与6的关系即可;
(3)把2010代入(2)得到的关系式,可结果是否为正整数即可.
(2)得到第n个图形中三角形的个数与6的关系即可;
(3)把2010代入(2)得到的关系式,可结果是否为正整数即可.
解答:解:(1)
;
(2)第2个图形中有6个三角形;
第3个图形中有6×2=12个三角形;
…
第n个图形中有6×(n-1)个三角形;
(3)6×(n-1)=2010,
解得n=336.
答:第336个图形中,能分出2010个三角形.
| 图形标号 | 1 | 2 | 3 |
| 正六边形个数 | 1 | 2 | 3 |
| 三角形个数 | 0 | 6 | 12 |
(2)第2个图形中有6个三角形;
第3个图形中有6×2=12个三角形;
…
第n个图形中有6×(n-1)个三角形;
(3)6×(n-1)=2010,
解得n=336.
答:第336个图形中,能分出2010个三角形.
点评:考查图形的变化规律;得到第n个图形中三角形的个数与6的关系是解决本题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目

 如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,重复上述过程,经过10次后,所得到的正六边形是原正六边形边长的
如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,重复上述过程,经过10次后,所得到的正六边形是原正六边形边长的
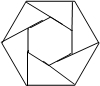 (2013•玉田县一模)如图,把正六边形各边按同一方向延长,使延长的线段长度与原正六边形的长度相等,顺次连接这六条线段外端点可以得到一个新的正六边形,重复上述过程,经过8次后,所得到的正六边形的边长是原六边形边长的
(2013•玉田县一模)如图,把正六边形各边按同一方向延长,使延长的线段长度与原正六边形的长度相等,顺次连接这六条线段外端点可以得到一个新的正六边形,重复上述过程,经过8次后,所得到的正六边形的边长是原六边形边长的 一个六棱柱模型如图所示,它的底面边长都是5cm,侧棱长4cm.
一个六棱柱模型如图所示,它的底面边长都是5cm,侧棱长4cm.