题目内容
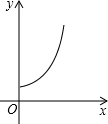
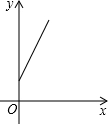
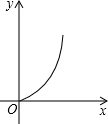
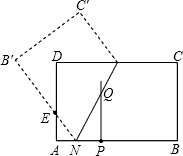
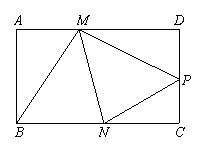
 已知:如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD上,且AE=1,点P是线段AB上一动点.折叠纸片,使点P与点E重合,展开纸片得折痕MN,过点P作PQ⊥AB,交MN所在的直线于点Q.设x=AP,y=PQ,则y关于x的函数图象大致为( )
已知:如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD上,且AE=1,点P是线段AB上一动点.折叠纸片,使点P与点E重合,展开纸片得折痕MN,过点P作PQ⊥AB,交MN所在的直线于点Q.设x=AP,y=PQ,则y关于x的函数图象大致为( )分析:易证△PFN∽△PAE∽△QPN,根据相似三角形对应边的比相等,即可求得y与x的函数关系式,利用函数的性质即可选择.
解答: 解:连接EP交NQ与点F,则NQ是EP的中垂线,
解:连接EP交NQ与点F,则NQ是EP的中垂线,
在直角△AEP中,EP=
=
,
则EF=PF=
,
∵∠A=∠NFP=90°,∠NPF=∠EPA,
∴△PFN∽△PAE,
∴
=
,即
=
,
则PN=
,
∵直角△NPQ中,PF⊥NQ,
∴△QPN∽△PFN
∴△QPN∽△PAE,
∴
=
,即
=
,则y=
x2+
.
则函数图象是D.
故选D.
 解:连接EP交NQ与点F,则NQ是EP的中垂线,
解:连接EP交NQ与点F,则NQ是EP的中垂线,在直角△AEP中,EP=
| AE2+AP2 |
| x2+1 |
则EF=PF=
| ||
| 2 |
∵∠A=∠NFP=90°,∠NPF=∠EPA,
∴△PFN∽△PAE,
∴
| PF |
| PA |
| PN |
| PE |
| ||
| 2x |
| PN | ||
|
则PN=
| x2+1 |
| 2x |
∵直角△NPQ中,PF⊥NQ,
∴△QPN∽△PFN
∴△QPN∽△PAE,
∴
| PQ |
| AP |
| PN |
| AE |
| y |
| x |
| x2+1 |
| 2x |
| 1 |
| 2 |
| 1 |
| 2 |
则函数图象是D.
故选D.
点评:本题考查了相似三角形的判定与性质,正确求得函数的解析式是关键.

练习册系列答案
相关题目
 已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD于点M,折痕交边BC于点N.
已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD于点M,折痕交边BC于点N.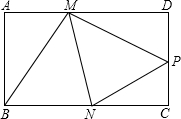 已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD于点M,折痕交边BC于点N.
已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD于点M,折痕交边BC于点N.