题目内容
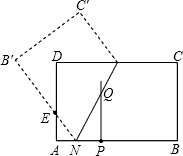
已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD与点M,折痕交边BC于点N .
(1)写出图中的全等三角形. 设CP=![]() ,AM=
,AM=![]() ,写出
,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)试判断∠BMP是否可能等于90°. 如果可能,请求出此时CP的长;如果不可能,请说明理由.
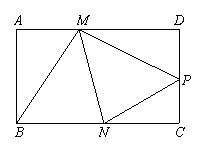
(1) ⊿MBN≌⊿MPN
∵⊿MBN≌⊿MPN
∴MB=MP,
∴![]()
∵矩形ABCD
∴AD=CD (矩形的对边相等)
∴∠A=∠D=90°(矩形四个内角都是直角)
∵AD=3, CD=2, CP=x, AM=y
∴DP=2-x, MD=3-y
Rt⊿ABM中,
![]()
同理 ![]() …
…
![]()
∴ ![]()
(3)![]()
当![]() 时,
时,
可证![]()
∴ AM=CP,AB=DM
∴ ![]()
∴ ![]()
∴当CM=1时,![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
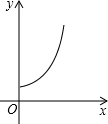
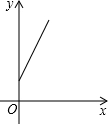
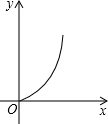
 已知:如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD上,且AE=1,点P是线段AB上一动点.折叠纸片,使点P与点E重合,展开纸片得折痕MN,过点P作PQ⊥AB,交MN所在的直线于点Q.设x=AP,y=PQ,则y关于x的函数图象大致为( )
已知:如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD上,且AE=1,点P是线段AB上一动点.折叠纸片,使点P与点E重合,展开纸片得折痕MN,过点P作PQ⊥AB,交MN所在的直线于点Q.设x=AP,y=PQ,则y关于x的函数图象大致为( ) 已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD于点M,折痕交边BC于点N.
已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD于点M,折痕交边BC于点N.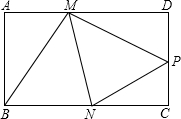 已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD于点M,折痕交边BC于点N.
已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD于点M,折痕交边BC于点N.