题目内容
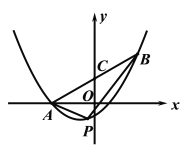
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与x轴交于A、B两点,与轴交于点
与x轴交于A、B两点,与轴交于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求抛物线的函数表达式;
(2)抛物线的对称轴与x轴交于点D,连接![]() ,点E为第三象限抛物线上的一动点,
,点E为第三象限抛物线上的一动点,![]() ,直线
,直线![]() 与抛物线交于点F,设直线
与抛物线交于点F,设直线![]() 的表达式为
的表达式为![]() .
.
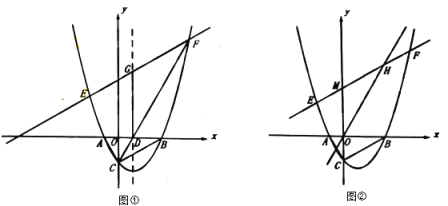
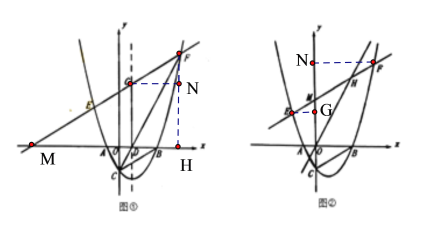
①如图①,直线![]() 与抛物线对称轴交于点G,若
与抛物线对称轴交于点G,若![]() ,求k、b的值;
,求k、b的值;
②如图②,直线![]() 与y轴交于点M,与直线
与y轴交于点M,与直线![]() 交于点H,若
交于点H,若![]() ,求b的值.
,求b的值.
【答案】(1)![]() ;(2)①k=
;(2)①k=![]() ,b=
,b=![]() ,②
,②![]() .
.
【解析】
(1)把![]() 代入
代入![]() ,求出a的值,即可;
,求出a的值,即可;
(2)①由![]() ,DG=FG,由
,DG=FG,由![]() ,∠GMD=∠OBC=30°,过点G作GN∥x轴,过点F作FN∥y轴,交于点N,交x轴于点H,则∠FGN=30°,设DG=FG=m,得:点F坐标是:(1+
,∠GMD=∠OBC=30°,过点G作GN∥x轴,过点F作FN∥y轴,交于点N,交x轴于点H,则∠FGN=30°,设DG=FG=m,得:点F坐标是:(1+![]() ,
,![]() ),代入二次函数得解析式,可得:点F坐标是:(5,
),代入二次函数得解析式,可得:点F坐标是:(5,![]() ),由∠GMD=30°和待定系数法,分别可得k,b的值;
),由∠GMD=30°和待定系数法,分别可得k,b的值;
②由直线![]() 与y轴交于点M,与直线
与y轴交于点M,与直线![]() 交于点H,
交于点H,![]() ,可得:
,可得:![]() ,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,MH=MO=b,作EG⊥y轴,FN⊥y轴,则,ME=
,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,MH=MO=b,作EG⊥y轴,FN⊥y轴,则,ME=![]() EG,MF=
EG,MF=![]() FN,设点E,F的很坐标分别是:
FN,设点E,F的很坐标分别是:![]() ,
,![]() ,由
,由![]() ,得到关于b的方程,即可求解.
,得到关于b的方程,即可求解.
(1)把![]() 代入
代入![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∴抛物线的函数表达式为:![]() ;
;
(2)① 由第(1)题,可知:A(-1,0),B(3,0),![]() ,
,
∴OB=3,OC=![]() ,BC=
,BC=![]() =
=![]() ,
,
∴∠OBC=30°,
∵抛物线的对称轴与x轴交于点D,
∴D坐标为(1,0),即OD=1,BD=2,
∴CD=![]() ,
,
∴BD=CD,
∵![]() ,
,
∴DG=FG,
∵![]() ,
,
∴∠GMD=∠OBC=30°,
过点G作GN∥x轴,过点F作FN∥y轴,交于点N,交x轴于点H,则∠FGN=30°,如图①,
设DG=FG=m,则![]() ,
,![]() ,
,![]() ,
,
∴FH=FN+NH=![]() ,OH=OD+DH=1+
,OH=OD+DH=1+![]() ,
,
∴点F坐标是:(1+![]() ,
,![]() ),
),
∴![]() ,解得:
,解得:![]() ,
,![]() (舍)
(舍)
∴点F坐标是:(5,![]() ),
),
∵∠GMD=30°,可设直线![]() 的表达式为
的表达式为![]() ,
,
把(5,![]() )代入
)代入![]() ,得:
,得:![]() ,解得:b=
,解得:b=![]() ,
,
∴直线![]() 的表达式为:
的表达式为:![]() ,即:k=
,即:k=![]() ,b=
,b=![]() .
.
②∵直线![]() 与y轴交于点M,与直线
与y轴交于点M,与直线![]() 交于点H,
交于点H,![]() ,
,
∴![]() ,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,
,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,
∴MH=MO=b,
作EG⊥y轴,FN⊥y轴,则,ME=![]() EG,MF=
EG,MF=![]() FN,
FN,
设点E,F的很坐标分别是:![]() ,
,![]()
联立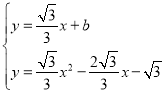 ,得:
,得:![]() ,
,
化简得:![]() ,
,
∴![]() +
+![]() =3,
=3,![]()
![]() =
=![]() ,
,
∵![]() ,
,
∴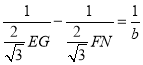 ,即:
,即: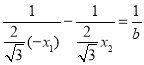 ,
,
化简得: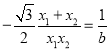 ,
,
∴![]() ,解得:b=
,解得:b=![]()

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案