题目内容
12．先化简，再求值：$\frac{1}{{a}^{2}-4a+4}$，其中a是一元二次方程x（x-2）=2-x的根．分析 通过解关于a的一元二次方程a（a-2）=2-a求得a的值，然后将其代入整理后的所求代数式进行求值，注意：分式的分母不等于零．
解答 解：原式=$\frac{1}{{{{（a-2）}^2}}}$．
∵a是一元二次方程x（x-2）=2-x的根
∴a（a-2）=2-a，
a（a-2）+a-2=0，
（a-2）（a+1）=0，
解得a1=2，a2=-1．
∵原分式中a≠2
∴a=-1
∴原式=$\frac{1}{9}$．
点评 本题考查了分式的化简求值．此题属于易错题，同学们解题时往往忽略了分母（a-2）2≠0这一条件．
练习册系列答案
相关题目
2．
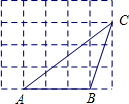如图，在5×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则sinA的值为（ ）
如图，在5×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则sinA的值为（ ）| A． | 1 | B． | $\frac{3}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
7．倒数是-3的数是（ ）
| A． | -3 | B． | 3 | C． | $\frac{1}{3}$ | D． | $-\frac{1}{3}$ |
如图所示，并按要求作图：