题目内容
1.若△ABC内接于⊙O,∠AOB=100°,求圆周角∠ACB的度数.分析 分点C在优弧和劣弧上两种情况,当点C在优弧上时,可直接利用圆周角定理得到∠ACB是∠AOB的一半,当点C在劣弧上时,可以优弧上找点D,则可求得∠ADB是∠AOB的一半,再利用圆内接四边形的性质可求得∠ACB
解答 解:如图1,当点C在优弧上时,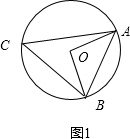
则∠ACB=$\frac{1}{2}$∠AOB=50°;
如图2,当点C在劣弧上时,在优弧上找点D,连接DA、DB,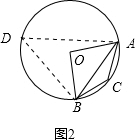
则可得∠ADB=$\frac{1}{2}$∠AOB=50°,
又∵四边形ACBD为圆的内接四边形,
∴∠ADB+∠ACB=180°,
∴∠ACB=180°-50°=130°,
∴∠ACB的度数是50°或130°.
点评 本题主要考查圆周角定理、圆内接四边形的性质,分点C在优弧和劣弧上两种情况进行讨论是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
9.射线OC,OD分别是∠AOB的三等分线,且OC,OD分别垂直于∠AOB的两边,那么∠AOB为( )
| A. | 90° | B. | 112.5° | C. | 135° | D. | 120° |
 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C. 苹果熟了,一个苹果从树上被抛下.如图所示,从A处落到了B处.(网格单位长度为1)
苹果熟了,一个苹果从树上被抛下.如图所示,从A处落到了B处.(网格单位长度为1)