Question

【题目】新定义：对非负数“四舍五入”到个位的值记为，即当为非负整数时，若，则如：，试解决下列问题

（1）填空：① ②若，则实数的取值范围为

（2）在关于的方程组中，若未知数满足，求的值．

（3）当时，若，求的最小值．

（4）求满足的所有非负实数的值，请直接写出答案 ．

Answer 1

【答案】（1）①3；②；（2）2；（3）0；（4）0或

【解析】

（1）①利用对非负实数x“四舍五入”到个位的值记为，进而得出的值；

②利用对非负实数x“四舍五入”到个位的值记为，且值为3，进而得出x的取值范围；

（2）根据方程组得到x+y的值，再利用得出m的范围，从而根据题干中的意义得出结果；

（3）根据得出x的取值范围，据此求出中y的最小值；

（4）利用，设，k为整数，得出关于k的不等关系求出即可．

解：（1）①由题意可得：3；

②∵，

∴

∴；

（2）∵，

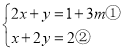①+②得：，

∴，

∵，

∴，

解得：，

∴=2；

（3）∵，

∴，

∴，

当x=时，y最小，且为0；

（4）设，k为整数，则，

∴，

∴，k≥0，

∴，

∴k=0，1，

则x=0或.