Question

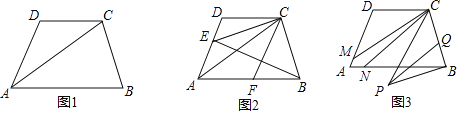
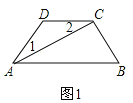
【题目】如图1四边形中，平分，；

（1）试说明与的位置关系,并予以证明：

（2）如图2，若，作平分交于，平分交于，求的度数．

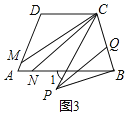
（3）如图3，若若是下一点，平分，，平分若下列结论：①的值不变;②的度数不变；可以证明只有一个是正确的，请你作出正确的选择并求值．

Answer 1

【答案】（1）AB∥CD，理由见解析；（2）45°；（3）②正确，14°

【解析】

（1）根据内错角相等，两直线平行进行证明即可；
（2）设∠DCE=∠ACE=α，则∠CAB=2α，根据∠ACB=∠ABC，可得∠ACB=90°-α，进而得到∠BCE=90°，最后根据CF平分∠ECB，可得∠ECF=∠BCE=45°；
（3）根据三角形的一个外角等于与它不相邻的两个内角的和，可得∠1=∠BPC+∠ABP，再根据平行线的性质以及角平分线的定义表示出∠MCP、∠DPQ，根据两直线平行，内错角相等可得∠NCP=∠CPQ，然后列式表示出∠MCN=∠ABP，从而判定②正确．

解：（1）如图1，AB∥CD．
证明：∵AC平分∠DAB，
∴∠1=∠CAB，
∵∠1=∠2，
∴∠2=∠CAB，
∴AB∥CD；

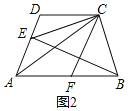
（2）∵CE平分∠DCA，AB∥CD，
∴可设∠DCE=∠ACE=α，则∠CAB=2α，
∵∠ACB=∠ABC，
∴△ABC中，∠ACB=（180°-∠CAB）=90°-α，
∴∠BCE=∠BCA+∠ECA=90°-α+α=90°，
∵CF平分∠ECB，
∴∠ECF=∠BCE=45°；

（3）结论②正确．
如图，根据三角形的外角性质可得，∠1=∠BPC+∠ABP，
∵PQ平分∠BPC，CM平分∠DCP，
∴∠CPQ=∠BPC，∠MCP=∠DCP．
∵AB∥CD，
∴∠1=∠DCP，
∴∠MCP=（∠BPC+∠ABP），
∵PQ∥CN，
∴∠NCP=∠CPQ=∠BPC，
∴∠MCN=∠MCP-∠NCP=（∠BPC+∠ABP）-∠BPC=∠ABP=×28°=14°，
∴结论②∠MCN的度数不变，为14°．