Question

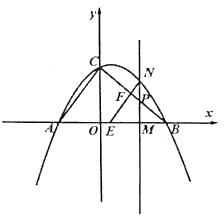
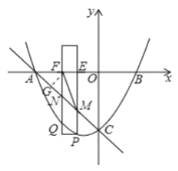
【题目】如图，抛物线与轴交于点和点，与轴交于点，点的坐标为，点的坐标为.有一宽度为1，长度足够长的矩形（阴影部分）沿轴方向平移，与轴平行的一组对边交抛物线于点和点，交直线于点和点，交轴于点和点.

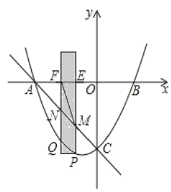
（1）求抛物线的解析式及点的坐标；

（2）当点和都在线段上时，连接，如果，求点的坐标；

（3）在矩形的平移过程中，是否存在以点，，，为顶点的四边形是平行四边形，若存在，求出点的坐标；若不存在，请说明理由.

Answer 1

【答案】（1），的坐标是；（2）点坐标；（3）点，，，为顶点的四边形是平行四边形时，点的坐标为或或.

【解析】

（1）将点B的坐标、点C的坐标分别代入函数解析式求得b、c的值，结合抛物线解析式求得点A的坐标；

（2）作FG⊥AC于G，设点F坐标（m，0），根据sin∠AMF=，列出方程即可解决问题．

（3））①当MN是对角线时，设点F（m，0），由QN=PM，列出方程即可解决问题．②当MN为边时，设点Q（m，）则点P（m+1，），代入抛物线解析式，解方程即可．

（1）抛物线上的点的坐标为，点的坐标为

将其代入，得，

解得，.

抛物线的解析式为.

点的坐标是.

（2）作于，设点坐标，

则，，，

，

，

，

，

整理得到，

，

或（舍弃），

点坐标.

（3）①当是对角线时，点在轴的右侧，设点，

直线解析式为，

点，点，

，

，

解得或（舍弃），

此时，

当是对角线时，点在点的左侧时，设点.

.

解得或（舍弃），

此时；

②当为边时，设点，则点，

，

，

解得.

点坐标，

综上所述，以点，，，为顶点的四边形是平行四边形时，点的坐标为或或.