题目内容
【题目】已知直线![]() 可变形为:
可变形为:![]() ,则点P(
,则点P(![]() )到直线
)到直线![]() 的距离d可用公式
的距离d可用公式![]() 计算.
计算.
例如:求点P(-2,1)到直线![]() 的距离.
的距离.
解:因为直线![]() 可变形为
可变形为![]() ,其中
,其中![]() ,
,![]() .
.
所以点P(-2,1)到直线![]() 的距离为
的距离为![]() .
.
根据以上材料求:
(1)点P(2,-1)到直线![]() 的距离;
的距离;
(2)已知M为直线![]() 上的点,且M到直线
上的点,且M到直线![]() 的距离为
的距离为![]() ,求M的坐标;
,求M的坐标;
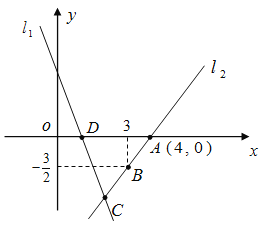
(3)已知线段![]() 上的点到直线
上的点到直线![]() 的最小距离为1,求k的值.
的最小距离为1,求k的值.
【答案】(1)![]() ;(2)M(6,-4)或M(-4,6);(3)
;(2)M(6,-4)或M(-4,6);(3)![]() 或
或![]()
【解析】(1)将P的坐标代入点到直线的距离公式即可直接求出答案;
(2)利用距离公式建立方程即可求解;
(3)利用点到直线的距离公式和待定系数法即可求出答案.
(1)直线![]() 化为:
化为:![]() ,其中
,其中![]()
![]()
(2)设M(![]() ),直线
),直线![]() 化为:
化为:![]() ,其中k=2,
,其中k=2,![]() ,故M到直线的距离为:
,故M到直线的距离为:
![]()
∴![]()
∴![]() 或
或![]()
∴M(6,-4)或M(-4,6)
(3)设![]() 上到直线
上到直线![]() 距离为1的点为(
距离为1的点为(![]() )或(
)或(![]() )
)
直线![]() 化为
化为![]() ,其中
,其中![]()
把(![]() )代入
)代入
![]() ,
,![]()
故![]()
∵直线![]() 与
与![]() 的交点横坐标为
的交点横坐标为![]()
∴![]()
同理,将(![]() )代入距离公式,得
)代入距离公式,得
![]() (
(![]() 舍去)
舍去)
综上所述,![]() 或
或![]()

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目